Capítulo 9 Medición de la utilidad y la pérdida de información
Hoy en día, resolver la tensión entre la protección de la información personal y el suministro de datos es realmente un desafío que deben asumir las ONE. En esta situación, tres motivaciones empujan a las ONE a preservar la confidencialidad.
SDC es un intercambio entre el riesgo de divulgación versus la pérdida de utilidad de los datos (siempre buscando minimizar este último), al tiempo que reduce el riesgo de divulgación a un nivel aceptable. La utilidad de los datos en este contexto significa la utilidad de los datos anonimizados para los análisis estadísticos de los usuarios finales, así como la validez de estos análisis cuando se realizan con datos anonimizados. El riesgo de divulgación y su medición se definirán más adelante en Medición de riesgos.
Para lograr este equilibrio entre minimizar el riesgo de divulgación y maximizar la utilidad de los datos para los usuarios finales, es necesario medir la utilidad de los datos después de la anonimización y compararla con la utilidad de los datos originales.
En esta sección se busca describir las medidas que se pueden usar para comparar la utilidad de los datos antes y después de la anonimización, así como también cuantificar la pérdida de información. La pérdida de información es inversa a la utilidad de los datos: cuanto mayor sea la utilidad de los datos después de la anonimización, menor será la pérdida de información.
Nota 1. Si los microdatos a anonimizar se basan en una muestra, los datos incurrirán en un error de muestreo. También pueden estar presentes otros errores en los datos, como un error de falta de respuesta. 2. Los métodos discutidos aquí solo miden la pérdida de información causada por el proceso de anonimización en relación con los datos de la muestra original y no intentan medir el error causado por otras fuentes.
La pérdida de información se evalúa con respecto a las necesidades y usos de los usuarios finales de los microdatos. Sin embargo, los diferentes usuarios de los datos anonimizados pueden tener usos muy diversos para los datos publicados y es posible que no sea posible recopilar una lista exhaustiva de los distintos usos. Es así que nos enfocaremos en la publicación de un conjunto de datos para evitar la divulgación no intencional. La publicación de múltiples conjuntos de datos anónimos para diferentes propósitos puede dar lugar a una divulgación no intencionada.36
El proceso SDC se caracteriza por el balance entre el riesgo de divulgación y la utilidad de los datos para los usuarios finales. La escala riesgo-utilidad se extiende entre dos extremos:
- No se difunden datos (riesgo cero de divulgación) y, por lo tanto, los usuarios no obtienen ninguna utilidad de los datos.
- Los datos se difunden sin ningún tratamiento y, por lo tanto, con el máximo riesgo de divulgación, pero con la máxima utilidad para el usuario (es decir, sin pérdida de información).
El objetivo de un proceso SDC bien implementado es encontrar el punto óptimo en el que la utilidad para los usuarios finales se maximice a un nivel de riesgo aceptable.
En el balance entre Riesgo y Utilidad que se muestra en la Figura @ref(fig:fig1_sec05), por un extremo, el triángulo corresponde a los datos sin procesar, los que no tienen pérdida de información, pero generalmente tienen un riesgo de divulgación más alto que el nivel aceptable. El otro extremo es el cuadrado, que corresponde a la no publicación de datos. En ese caso, no hay riesgo de divulgación, pero tampoco hay utilidad de los datos para los usuarios. Los puntos intermedios corresponden a diferentes opciones de métodos SDC y/o parámetros aplicados a diferentes variables. El proceso SDC busca métodos y parámetros, que son aplicados de una manera que produce una reducción del riesgo de forma muchas veces satisfactoria, minimizándose generalmente la pérdida de información.
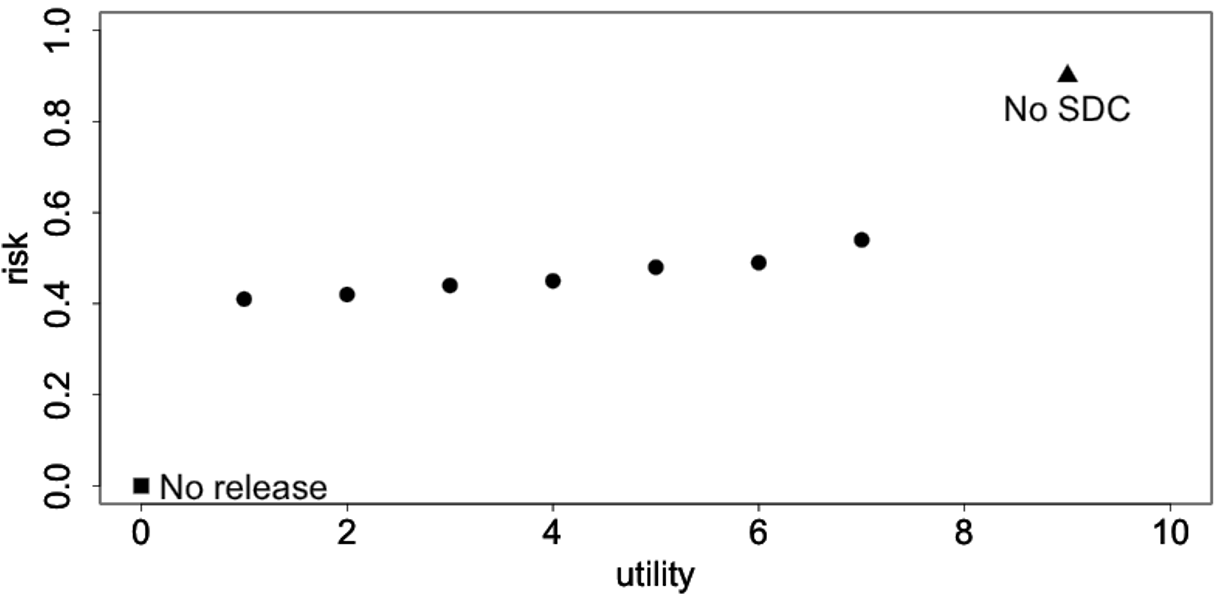
(#fig:fig1_sec05)Balance riesgo-utilidad en un conjunto de datos.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.78.
En las siguientes secciones, primero proponemos medidas generales de utilidad independientes del uso de datos, y luego presentamos un ejemplo de una medida específica útil para medir la pérdida de información con respecto a usos de datos específicos. Finalmente, mostramos cómo visualizar cambios en los datos causados por la anonimización y discutimos la selección de medidas de utilidad para un conjunto de datos en particular.
9.1 Medidas generales de utilidad para variables continuas y categóricas
Las medidas generales de pérdida de información se pueden dividir en aquellas que comparan los valores reales de los datos sin procesar y los anonimizado, y aquellas que comparan las estadísticas de ambos conjuntos de datos. Todas las medidas son a posteriori, ya que miden la utilidad después de la anonimización y requieren tanto los datos originales como los anonimizados.
Las medidas de utilidad son diferentes para variables categóricas y para las variables continuas.
9.1.1 Variables categóricas
9.1.1.1 Número de valores faltantes
Una medida informativa es comparar el número de valores faltantes en los datos. Los valores faltantes a menudo se producen después de la supresión y a mayor cantidad de aplicación de supresiones será mayor el grado de pérdida de información. Después de usar la función de supresión local en un objeto sdcMicro , la cantidad de supresiones para cada variable clave categórica se puede recuperar con la función print(), como se muestra en el Bloque 9.137. El argumento ‘ls’ en la función print() es la supresión local. La salida muestra el número absoluto y relativo de supresiones.
Bloque 9.1 Uso de la función print() para recuperar el número total de supresiones para cada variable clave categórica
sdcInitial <- localSuppression(sdcInitial, k = 5, importance = NULL)
print(sdcInitial, 'ls')
## Local Suppression:
## KeyVar | Suppressions (#) | Suppressions (%)
## URBRUR | 0 | 0.000
## REGION | 81 | 4.050
## RELIG | 0 | 0.000
## MARITAL | 0 | 0.000
## --------------------------------------------------------------Es posible contar y comparar el número de valores faltantes en los datos originales y los datos tratados. Esto puede ser útil para ver el aumento proporcional en el número de valores faltantes. Los valores faltantes
también pueden tener otras fuentes, como la no respuesta. En el Bloque 9.2 se muestran los valores faltantes para cada una de las variables clave categóricas en un objeto sdcMicro. Aquí se utiliza el supuesto que todos los valores faltantes están codificados como NA. Si los valores perdidos no están codificados como NA, sino otro valor, se debe utilizar el código de valores perdidos alternativo. Los resultados concuerdan con el número de valores faltantes introducidos por la supresión local en el ejemplo anterior, pero también muestran que la variable “RELIG” tiene 1000 valores faltantes en los datos originales.
Bloque 9.2 Número de valores faltantes para cada variable clave categórica en un objeto sdcMicro
# Almacene los nombres de todas las variables clave categóricas en un vector
namesKeyVars <- names(sdcInitial@manipKeyVars)
# Elaborar una matriz para almacenar el número de valores faltantes (NA) antes y después de la anonimización
NAcount <- matrix(NA, nrow = 2, ncol = length(namesKeyVars))
colnames(NAcount) <- c(paste0('NA', namesKeyVars)) # column names
rownames(NAcount) <- c('initial', 'treated') # row names
# Recuento de NA en todas las variables clave (NOTA: solo se cuentan las codificadas como NA)
for(i in 1:length(namesKeyVars)) {
NAcount[1, i] <- sum(is.na(sdcInitial@origData[,namesKeyVars[i]]))
NAcount[2, i] <- sum(is.na(sdcInitial@manipKeyVars[,i]))
}
# Mostrar resultados
NAcount
## NAURBRUR NAREGION NARELIG NAMARITAL
## inicial 0 0 1000 51
## tratado 0 81 1000 519.1.1.2 Número de registros cambiados
Otra estadística útil es el número de registros modificados por variable. Estos se pueden contabilizar de forma similar a los valores perdidos e incluyen supresiones (es decir, cambios en los valores perdidos/NA en R ). El número de registros cambiados es un buen indicador del impacto de los métodos de anonimización en los datos. A
continuación en el Bloque 9.3 se muestra cómo calcular la cantidad de registros modificados para las variables PRAMmed.
Bloque 9.3 Cálculo del número de registros modificados por variable
# Almacene los nombres de todas las variables del pram en un vector
namesPramVars <- names(sdcInitial@manipPramVars)
# Marco para guardar la cantidad de registros modificados
recChanged <- rep(0, length(namesPramVars))
names(recChanged) <- c(paste0('RC', namesPramVars))
# Cuenta del número de registros cambiados
for(j in 1:length(namesPramVars)) # para todas las variables clave
{
comp <- sdcInitial@origData[namesPramVars[j]] !=
sdcInitial@manipPramVars[namesPramVars[j]]
temp1 <- sum(comp, na.rm = TRUE) # cambio en todas las variables sin NA
temp2 <- sum(is.na(comp)) # contabiliza los NA en el vector
temp3 <- sum(is.na(sdcInitial@origData[namesPramVars[j]])
+ is.na(sdcInitial@manipPramVars[namesPramVars[j]])==2)
# ambos NA, sin cambios, contabilizados en temp2
recChanged[j] <- temp1 + temp2 - temp3
}
# Mostrar resultados
recChanged
## RCWATER RCROOF RCTOILET
## 125 86 1809.1.1.3 Comparación de tablas de contingencia
Una forma útil de medir la pérdida de información en variables categóricas es comparar tabulaciones univariadas y, lo que es más interesante, tablas de contingencia (también tabulaciones cruzadas o tablas de doble entrada) entre pares de variables. Para mantener la validez analítica de un conjunto de datos, las tablas de contingencia
deben permanecer aproximadamente iguales. La función table() produce tablas de contingencia de una o más variables. El Bloque 9.4 a continuación crea una tabla de contingencia de las variables “REGION” y “URBRUR”. Observamos pequeñas diferencias entre las tablas antes y después de la anonimización.
Bloque 9.4 Comparación de tablas de contingencia de variables categóricas
# Tabla de contingencia (tabulación cruzada) de las variables region y urban/rural
table(sdcInitial@origData[, c('REGION', 'URBRUR')]) # antes de la anonimización
## URBRUR
## REGION 1 2
## 1 235 89
## 2 261 73
## 3 295 76
## 4 304 71
## 5 121 139
## 6 100 236
table(sdcInitial@manipKeyVars[, c('REGION', 'URBRUR')]) # después de la anonimización
## URBRUR
## REGION 1 2
## 1 235 89
## 2 261 73
## 3 295 76
## 4 304 71
## 5 105 130
## 6 79 201(J. Domingo-Ferrer and Torra 2001)proponen una medida de pérdida de información basada en tablas de contingencia, que cuantifica la distancia entre las tablas de contingencia en los datos originales y los tratados. Alternativamente, se pueden usar visualizaciones de la tabla de contingencia con gráficos de mosaico para comparar el impacto de los métodos de anonimización en las tabulaciones y tablas de contingencia (consulte la Gráficos de mosaico).
9.1.2 Variables continuas
9.1.2.1 Estadísticas: media, covarianza, correlación
Las estadísticas que caracterizan el conjunto de datos no deben cambiar después de la anonimización, como lo son la media, varianza, covarianza y la correlación entre las variables más importantes en el conjunto de datos. (J. Domingo-Ferrer and Torra 2001) da una visión general de las estadísticas que se pueden considerar. Para evaluar la pérdida de información causada por la anonimización, se deben comparar las estadísticas apropiadas para las variables continuas antes y después de la anonimización.
Para evaluar la pérdida de utilidad se cuentan con varias formas de cálculo, por ejemplo, comparando medias y (co-)varianzas en los datos o comparando las distribuciones (multivariadas) de los datos. Especialmente los cambios en las correlaciones brindan información valiosa sobre la validez de los datos para las regresiones. Las
funciones del paquete base R o cualquier otro paquete estadístico se pueden usar para hacer esto. Los siguientes son algunos ejemplos en R.
Para calcular la media de cada variable numérica usamos la función colMeans(). Para ignorar los valores perdidos, es necesario utilizar la opción na.rm = TRUE. “numVars” es un vector con los nombres de las variables numéricas. El Bloque 9.5 muestra cómo calcular las medias de todas las variables numéricas. Los datos no tratados se extraen de la ranura ‘origData’ del objeto sdcMicro y los datos anonimizados del slot ‘manipNumVars’, que contiene las variables numéricas manipuladas. Observamos pequeños cambios en cada una de las tres variables.
Bloque 9.5 Comparando las medias de variables continuas
# datos no tratados
colMeans(sdcInitial@origData[, numVars], na.rm = TRUE)
## INC INCRMT INCWAGE
## 479.7710 961.0295 1158.1330
# datos anonimizados
colMeans(sdcInitial@manipNumVars[, numVars], na.rm = TRUE)
## INC INCRMT INCWAGE
## 489.6030 993.8512 1168.7561De la misma manera, se pueden calcular las matrices de correlación y covarianza de las variables numéricas en el objeto sdcMicro a partir de los datos no tratados y anonimizados. Esto se muestra en el Bloque 9.6. Observamos que la varianza de cada variable (los elementos diagonales en la matriz de covarianza) ha aumentado por la anonimización. Estas funciones también permiten calcular intervalos de confianza en el caso de muestras. Las medias y las covarianzas de los subconjuntos de los datos tampoco deberían diferir. Un ejemplo es la media de ingresos por género, por grupo de edad o por región. Este tipo de características de los datos son importantes para el análisis.
Bloque 9.6 Comparación de estructuras de covarianza y matrices de correlación de variables numéricas
# datos no tratados
cov(sdcInitial@origData[, numVars])
## INC INCRMT INCWAGE
## INC 1645926.1 586975.6 2378901
## INCRMT 586975.6 6984502.3 1664257
## INCWAGE 2378900.7 1664257.4 16169878
cor(sdcInitial@origData[, numVars])
## INC INCRMT INCWAGE
## INC 1.0000000 0.1731200 0.4611241
## INCRMT 0.1731200 1.0000000 0.1566028
## INCWAGE 0.4611241 0.1566028 1.0000000
# datos anonimizados
cov(sdcInitial@manipNumVars[, numVars])
## INC INCRMT INCWAGE
## INC 2063013.1 649937.5 2382447
## INCRMT 649937.5 8566169.1 1778985
## INCWAGE 2382447.4 1778985.1 19925870
cor(sdcInitial@manipNumVars[, numVars])
## INC INCRMT INCWAGE
## INC 1.0000000 0.1546063 0.3715897
## INCRMT 0.1546063 1.0000000 0.1361665
## INCWAGE 0.3715897 0.1361665 1.0000000(J. Domingo-Ferrer and Torra 2001) propone varias medidas para la diferencia entre las matrices de covarianza y las de correlación. Estas medidas se basan en el error cuadrático medio, el error absoluto medio o la variación media de las celdas individuales. Nos referimos a (J. Domingo-Ferrer and Torra 2001) para obtener una descripción completa de estas medidas.
9.1.2.2 Medida de pérdida de información IL1s
Alternativamente, también podemos comparar los datos reales y cuantificar la distancia entre el conjunto de datos original \(X\) y el conjunto de datos tratado \(Z\). Aquí \(X\) y \(Z\) contienen sólo variables continuas. (Yancey, Winkler, and Creecy 2002) introduce la medida de distancia IL1s, que es la suma de las distancias absolutas entre las observaciones correspondientes en los conjuntos de datos sin procesar y anónimos, que están estandarizados por la desviación estándar de las variables en los datos originales. Para las variables continuas en el conjunto de datos, la medida IL1s se define como:
\[IL1s=\frac{1}{pn}\sum_{j=1}^{p} \sum_{i=1}^{n} \frac{|xij−zij|} {\sqrt2S_1} \]
Donde \(p\) es el número de variables continuas; \(n\) es el número de registros en el conjunto de datos; \(xij\) y \(zij\), son los valores antes y después de la anonimización de la variable \(j\) e \(i\); Sj es la desviación estándar de la variable \(j\) en los datos originales (Yancey, Winkler, and Creecy 2002).
Cuando se usa sdcMicro, la medida de utilidad de datos IL1s se pueden calcular para todos los cuasi-identificadores numéricos con la función dUtility(), que se ilustra en el Bloque 9.7 a
continuación. En caso de ser necesario, también se puede calcular la medida en subconjuntos del conjunto completo de cuasi-identificadores numéricos. La función se llama dUtility(), pero devuelve una medida de pérdida de información. El resultado se guarda en la ranura de utilidad del objeto sdcMicro . El Bloque 9.7 a continuación ilustra cómo llamar al resultado.
Bloque 9.7 Uso de dUtility() para calcular la medida de utilidad de datos de IL1 en sdcMicro
# Evaluación de la medida IL1s para las variables en sdcMicro object sdcInitial
sdcInitial <- dUtility(sdcInitial)
# Mostrar los resultados de IL1s
sdcInitial@utility$il1
## [1] 0.2203791
# IL1s para un subconjunto numérico cuasi-identificadores
subset <- c('INCRMT', 'INCWAGE', 'INCFARMBSN')
dUtility(obj = sdcInitial@origData[,subset], xm = sdcInitial@manipNumVars[,subset],
method = 'IL1')
## [1] 0.5641103La medida es útil para comparar diferentes métodos. Cuanto menor sea el valor de la medida, más cerca estarán los valores de los valores originales y mayor será la utilidad.
Nota Esta medida está relacionada con las medidas de riesgo basadas en distancia e intervalos (ver la sección Medidas de riesgo para variables continuas) Cuanto mayor sea la distancia entre los valores originales y anonimizados, menor será la utilidad de los datos. Sin embargo, una mayor distancia también reduce el riesgo de re-identificación.
9.1.2.3 Valores propios
Otra forma de evaluar la pérdida de información es comparar los valores propios robustos de los datos antes y después de la anonimización. El Bloque 9.8 ilustra cómo usar este enfoque con sdcMicro . Aquí “contVars” es un vector con los nombres de las variables continuas que nos interesan. “obj” es el argumento que
especifica los datos no tratados y “xm” es el argumento que especifica los datos anonimizados. La salida de la función es la diferencia en valores propios. Por lo tanto, el valor mínimo es 0. Nuevamente, el uso principal es comparar diferentes métodos. Cuanto mayor sea el valor, mayores serán los cambios en los datos y la pérdida de información.
Bloque 9.8 Uso de dUtility() para calcular valores propios en sdcMicro
# Comparación de valores para variables continuas
dUtility(obj = sdcInitial@origData[,contVars],
xm = sdcInitial@manipNumVars[,contVars], method = 'eigen')
## [1] 2.482948
# Comparación de valores propios robustos de variables continuas*
dUtility(obj = sdcInitial@origData[,contVars],
xm = sdcInitial@manipNumVars[,contVars], method = 'robeigen')
## [1] -4.297621e+149.1.3 Medidas de utilidad basadas en las necesidades del usuario final
No se pueden catalogar todas las necesidades y usos de un determinado conjunto de datos. Sin embargo, algunos tipos de datos tienen usos similares o características importantes, que pueden evaluarse antes y después de la anonimización. Los ejemplos de “indicadores de evaluación comparativa” (Templ et al. 2014) son diferentes para cada conjunto de datos. Los ejemplos incluyen medidas de pobreza para conjuntos de datos de ingresos y tasas de asistencia escolar. A menudo, las ideas para seleccionar dichos indicadores provienen de los informes que publican los usuarios de datos basados en microdatos publicados anteriormente.
Como guía es necesario comparar los indicadores calculados sobre los datos no tratados y los datos después de la anonimización con diferentes métodos. Si las diferencias entre los indicadores no son demasiado grandes, el conjunto de datos anonimizados puede publicarse. Se debe tener en cuenta que los indicadores calculados sobre muestras son estimaciones con cierta varianza e intervalo de confianza. Por lo tanto, para datos de muestra, es informativo comparar la superposición de los intervalos de confianza y/o evaluar si la estimación puntual calculada después de la anonimización está contenida dentro del intervalo de confianza de la estimación original. Ejemplos de indicadores de referencia y sus intervalos de confianza y cómo calcularlos en R se incluyen en los estudios de casos de estas directrices. Aquí damos el ejemplo del coeficiente GINI.
El coeficiente de GINI es una medida de dispersión estadística, que a menudo se utiliza para medir la desigualdad de ingresos. Una forma de medir la pérdida de información en los datos de ingresos es comparar la distribución de ingresos, lo que se puede hacer fácilmente comparando los coeficientes de GINI. Varios paquetes de R tienen funciones para calcular el coeficiente GINI. Elegimos el paquete laeken, que calcula el coeficiente GINI como el área entre la línea de 45 grados y la curva de Lorenz. Para usar la función gini(), primero tenemos que instalar y cargar la paquete laeken. Para calcular el coeficiente de GINI para la variable, usamos los pesos de muestra en los datos. Esto se muestra en Bloque 9.9. El coeficiente de GINI de los datos de la muestra es una variable aleatoria. Por lo tanto, es útil construir un intervalo de confianza alrededor del coeficiente para evaluar la importancia de cualquier cambio en el coeficiente después de la anonimización. La función gini() calcula un intervalo de confianza de 1-alfa para el coeficiente de GINI mediante el uso de bootstrap.
Bloque 9.9 Cálculo del coeficiente de GINI a partir de la variable de ingresos para determinar la desigualdad de ingresos
# Coeficiente de Gini antes de la anonimización
gini(inc = sdcInitial@origData[selInc,'INC'],
weights = curW[selInc], na.rm = TRUE)$value # antes
## [1] 34.05928
# Coeficiente de Gini después de la anonimización
gini(inc = sdcInitial@manipNumVars[selInc,'INC'],
weights = curW[selInc], na.rm = TRUE)$value # después
## [1] 67.132189.1.4 Regresión
Además de comparar matrices de covarianza y correlación, las regresiones son una herramienta útil para evaluar si la estructura de los datos se mantiene después de la anonimización. Al comparar los parámetros de regresión, también es posible comparar relaciones entre variables no continuas (por ejemplo, al introducir variables ficticias o regresión con variables ordinales). Si se sabe con qué propósito y en qué campo se usan los datos, se pueden usar regresiones para comparar el cambio en los coeficientes y los intervalos de confianza.
Un ejemplo de la regresión para evaluar la utilidad de los datos en los datos de ingresos es la ecuación de Mincer. La ecuación de Mincer explica los ingresos en función de la educación y la experiencia mientras controla otras variables. La ecuación de Mincer se utiliza a menudo para evaluar la brecha salarial de género y la desigualdad salarial de género mediante la inclusión de una variable ficticia de género. Aquí mostramos cómo evaluar el impacto de los métodos de anonimización en el coeficiente de género. Realizamos una regresión del ingreso logarítmico en una constante, una variable ficticia de género, años de educación, años de experiencia, años de experiencia al cuadrado y otros factores que influyen en el salario.
\[ln(wage)=β_0+β_1gender+β_2education+β_3experience+β_3experience^2+βX\]
El parámetro de interés aquí es \(β_1\), el efecto del género en el logaritmo del salario. \(X\) es una matriz con varios otros factores que influyen en el salario y \(β\) los coeficientes de estos factores. El Bloque 9.10 ilustra cómo ejecutar una regresión de Mincer en \(R\) usando la función \(ln()\) y la evaluación de los coeficientes y los intervalos de confianza alrededor de los coeficientes. Realizamos la regresión como se especifica para los empleados asalariados con un salario positivo en los grupos de edad de 15 a 65 años.
Bloque 9.10 Estimación de la ecuación de Mincer (regresión) para evaluar la utilidad de los datos antes y después de la anonimización
# Variables de la ecuación de Mincer antes de la anonimización
Mlwage <- log(sdcMincer@origData$wage) # salario de registro
# TRUE if 'paid employee', else FALSE or NA
Mempstat <- sdcMincer@origData$empstat=='Paid employee'
Mage <- sdcMincer@origData$age # edad en años
Meducy <- sdcMincer@origData$educy # educación en años
Mexp <- sdcMincer@origData$exp # experiencia en años
Mexp2 <- Mexp^2 # experiencia al cuadrado
Mgender <- sdcMincer@origData$gender # variable ficticia de género
Mwgt <- sdcMincer@origData$wgt # variable de género para la regresión
MfileB <- as.data.frame(cbind(Mlwage, Mempstat, Mage, Meducy, Mexp, Mexp2,
Mgender, Mwgt))
# Variables de la ecuación de Mincer después de la anonimización
Mlwage <- log(sdcMincer@manipNumVars$wage) # salario de registro
Mempstat <- sdcMincer@manipKeyVars$empstat=='Paid employee'
# TRUE if 'paid employee', else FALSE or NA
Mage <- sdcMincer@manipKeyVars$age # edad en años
Meducy <- sdcMincer@manipKeyVars$educy # educación en años
Mexp <- sdcMincer@manipKeyVars$exp # experiencia en años
Mexp2 <- Mexp^2 # experiencia al cuadrado
Mgender <- sdcMincer@manipKeyVars$gender # variable ficticia de género
Mwgt <- sdcMincer@origData$wgt # variable de género para la regresión
MfileA <- as.data.frame(cbind(Mlwage, Mempstat, Mage, Meducy, Mexp, Mexp2,
Mgender, Mwgt))
# Fórmula de regresión
Mformula <- 'Mlwage ~ Meducy + Mexp + Mexp2 + Mgender'
# Regresión con la ecuación de Mincer
mincer1565B <- lm(Mformula, data = subset(MfileB,
MfileB$Mage >= 15 & MfileB$Mage <= 65 & MfileB$Mempstat==TRUE &
MfileB$Mlwage != -Inf), na.action = na.exclude, weights = Mwgt) # antes
mincer1565A <- lm(Mformula,
data = subset(MfileA,
MfileA$Mage >= 15 & MfileA$Mage <= 65 &
MfileA$Mempstat==TRUE &
MfileA$Mlwage != -Inf),
na.action = na.exclude, weights = Mwgt) # después
# los objetos mincer1565B y mincer1565A con los resultados
# regresión antes y después de la anonimización
mincer1565B$coefficients # antes
## (Intercept) Meducy Mexp Mexp2 Mgender
## 3.9532064886 0.0212367075 0.0255962570 -0.0005682651 -0.4931289413
mincer1565A$coefficients # después
## (Intercept) Meducy Mexp Mexp2 Mgender
## 4.0526250282 0.0141090329 0.0326711056 -0.0007605492 -0.5393641862
# Intervalos de confianza al 95%
confint(obj = mincer1565B, level = 0.95) # antes
## 2.5 % 97.5 %
## (Intercept) 3.435759991 4.4706529860
## Meducy -0.018860497 0.0613339120
## Mexp 0.004602597 0.0465899167
## Mexp2 -0.000971303 -0.0001652273
## Mgender -0.658085143 -0.3281727396
confint(obj = mincer1565A, level = 0.95) # después
## 2.5 % 97.5 %
## (Intercept) 3.46800378 4.6372462758
## Meducy -0.03305743 0.0612754964
## Mexp 0.01024867 0.0550935366
## Mexp2 -0.00119162 -0.0003294784
## Mgender -0.71564602 -0.3630823543Si las nuevas estimaciones caen dentro del intervalo de confianza original y los intervalos de confianza nuevos y originales se superponen en gran medida, los datos pueden considerarse válidos para este tipo de regresión después de la anonimización. La Figura @ref(fig:fig2__sec05) muestra las estimaciones puntuales y los intervalos de confianza para el coeficiente de género en este intercambio para un conjunto de datos de ingresos de muestra y varios métodos y parámetros de SDC. El punto rojo y la barra de confianza (en la parte superior) corresponden a las estimaciones de los datos no tratados, mientras que las otras barras de confianza corresponden a los métodos SDC con diferentes parámetros. La anonimización reduce el número de re-identificaciones esperadas en los datos (eje izquierdo) y las estimaciones puntuales y los intervalos de confianza varían mucho para los diferentes métodos SDC. Elegiríamos un método que reduzca el número esperado de identificaciones, sin cambiar el coeficiente de género y con una gran superposición del intervalo de confianza con el intervalo de confianza estimado a partir de los datos originales.
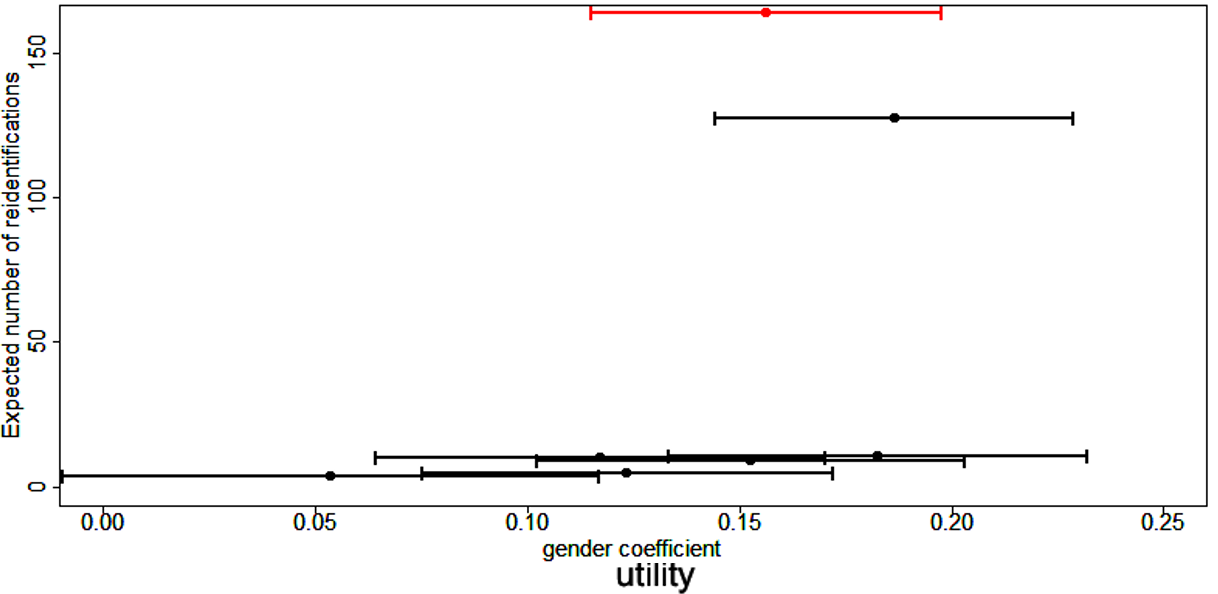
(#fig:fig2_sec05)Efecto de la anonimización en las estimaciones puntuales e intervalo de confianza del coeficiente de género en la ecuación de Mincer.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.90.
9.2 Evaluación de la utilidad de los datos con la ayuda de visualizaciones de datos (en R)
El uso de gráficos y otras técnicas de visualización, actúan como una buena forma de evaluar cuánto han cambiado los datos después de la anonimización ayudando a seleccionar las técnicas de anonimización adecuadas para los datos. Las visualizaciones pueden ser una herramienta útil para evaluar el impacto en la utilidad de los datos de los métodos de anonimización ya que facilitan la elección entre los métodos de anonimización. El lenguaje de programación R proporciona varias funciones y paquetes que pueden ayudar a visualizar los resultados de la
anonimización. Esta sección enumera algunas de estas funciones y paquetes y proporciona ejemplos de código para ilustrar cómo implementarlos. Se mostrarán las siguientes formas:
- histogramas y gráficos de densidad
- diagrama de caja
- gráfico en mosaico
Para hacer visualizaciones apropiadas, necesitamos usar los datos sin procesar y los datos anonimizados. Cuando se utiliza un objeto sdcMicro para el proceso de anonimización, los datos sin procesar se almacenan en la ranura “origData” del objeto y las variables anonimizadas están en las ranuras “manipKeyVars”, “manipPramVars”, “manipNumVars” y “manipStrataVar”. Consulte la sección Objetos de la clase sdcMicroObj para obtener más información sobre los objetos sdcMicro , los slots y cómo acceder a ellos.
9.2.0.1 Histogramas y gráficos de densidad
Son útiles para realizar comparaciones rápidas de la distribución de variables antes y después de la anonimización. La ventaja de los histogramas es que los resultados son exactos. Sin embargo, la visualización depende de los anchos de las barras y el inicio de la primera barra. Los histogramas se pueden utilizar para variables continuas y semicontinuas. Los gráficos de densidad muestran la densidad del kernel de los datos; por lo tanto, la gráfica depende del kernel que se elija y si los datos se ajustan bien al kernel. Sin embargo, los gráficos de densidad son una buena herramienta para ilustrar el cambio de valores y rangos de valores de variables continuas.
Los histogramas se pueden trazar con la función hist() y las densidades del kernel con las funciones plot() y density() en R . El Bloque 9.11 muestra ejemplos de cómo utilizar estas funciones para ilustrar los cambios en la variable “INC”, una variable de ingresos. La función hist() necesita como argumento los puntos de ruptura del histograma. Los resultados se muestran en la Figura @ref(fig:fig3_sec05) y la Figura @ref(fig:fig4_sec05). Los histogramas y los gráficos de densidad dan una indicación clara de cómo han cambiado los valores: la variabilidad de los datos ha aumentado y la forma de la distribución ha cambiado.
Bloque 9.11 Trazado de histogramas y densidades kernel
# Histograma
# gráfico de histograma antes de la anonimización
hist(sdcInitial@origData$INC, breaks = (0:180)*1e2,
main = "Histogram income - original data")
# gráfico de histograma después de la anonimización (adición de ruido)
hist(sdcInitial@manipNumVars$INC, breaks = (-20:190)*1e2,
main = "Histogram income - anonymized data")
# gráfico de densidades
# trazo de la curva de densidad original
plot(density(sdcInitial@origData$INC), xlim = c(0, 8000), ylim = c(0, 0.006),
main = "Density income", xlab = "income")
par (new = TRUE)
# trazo de la curva de densidad después de la anonimización (adición de ruido)
plot(density(sdcInitial@manipNumVars$INC), xlim = c(0, 8000), ylim = c(0, 0.006),
main = "Density income", xlab = "income")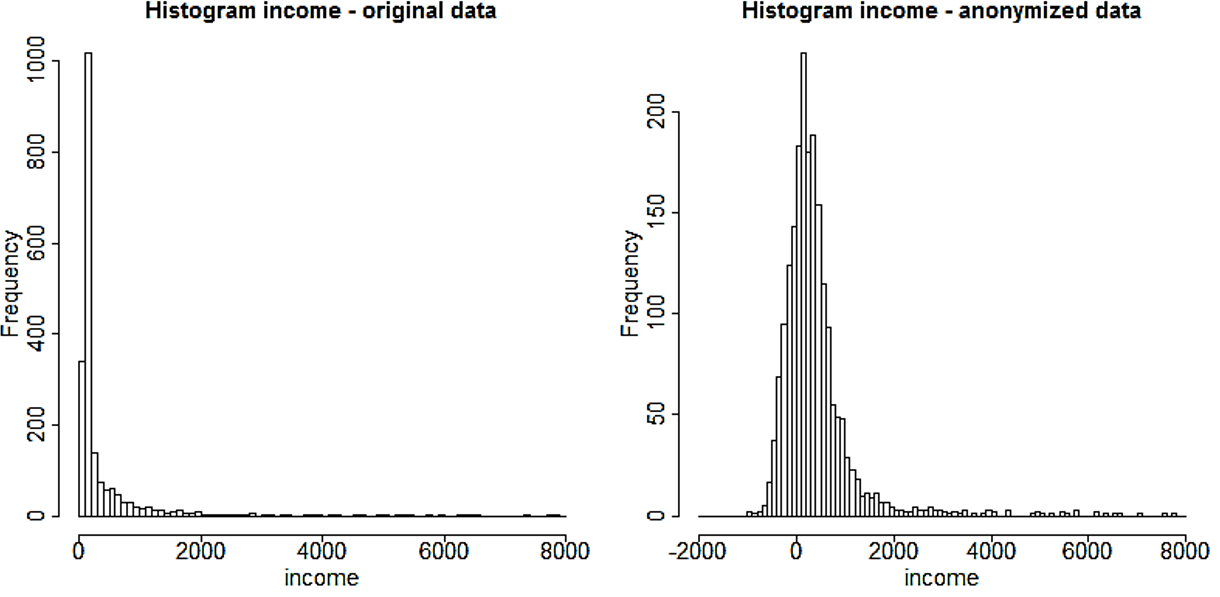
(#fig:fig3_sec05)Histogramas de ingresos antes y después de la anonimización.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.88.
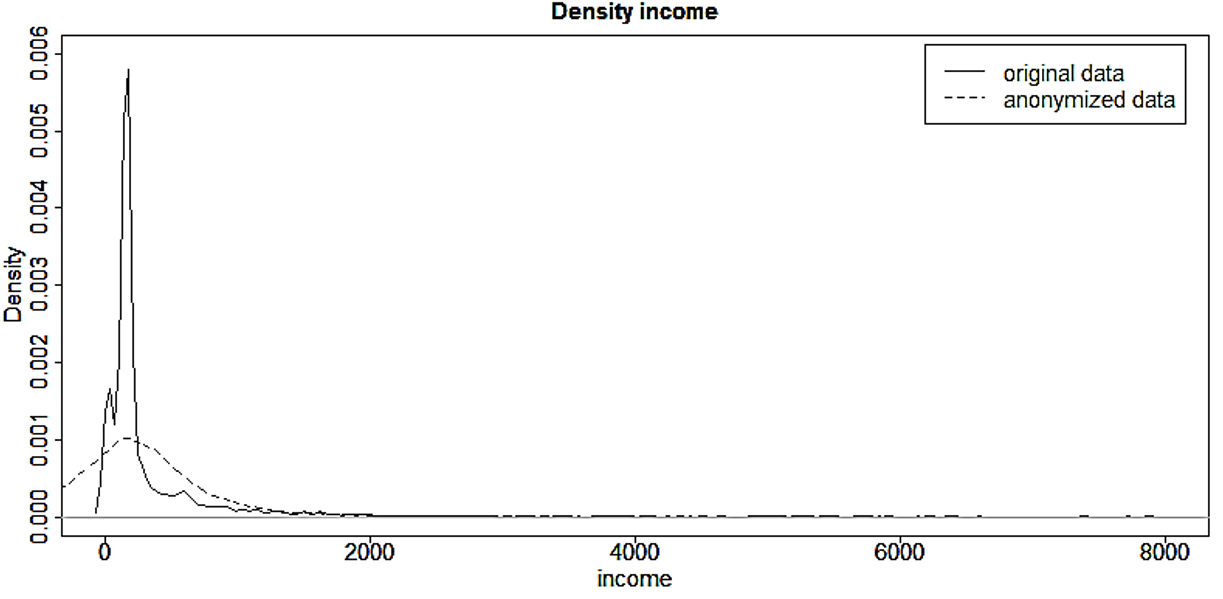
(#fig:fig4_sec05)Gráficas de densidad de ingresos antes y después de la anonimización.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.89.
9.2.0.2 Diagramas de caja
Los diagramas de caja brindan una descripción general rápida de los cambios en la dispersión y los valores atípicos de las variables continuas antes y después de la anonimización. El Bloque 9.12 a continuación muestra cómo generar diagramas de caja en R con la función boxplot(). resultado de la figura
@ref(fig:fig5_sec05) muestra un ejemplo de una variable de gasto después de agregar ruido. El diagrama de caja muestra claramente que la variabilidad en la variable gasto aumentó como resultado de los métodos de anonimización aplicados.
Bloque 9.12 Creación de diagramas de caja para variables continuas
boxplot(sdcObj@origData$TOTFOOD, sdcObj@manipNumVars$TOTFOOD,
xaxt = 'n', ylab = "Expenditure")
axis(1, at = c(1,2), labels = c('before', 'after'))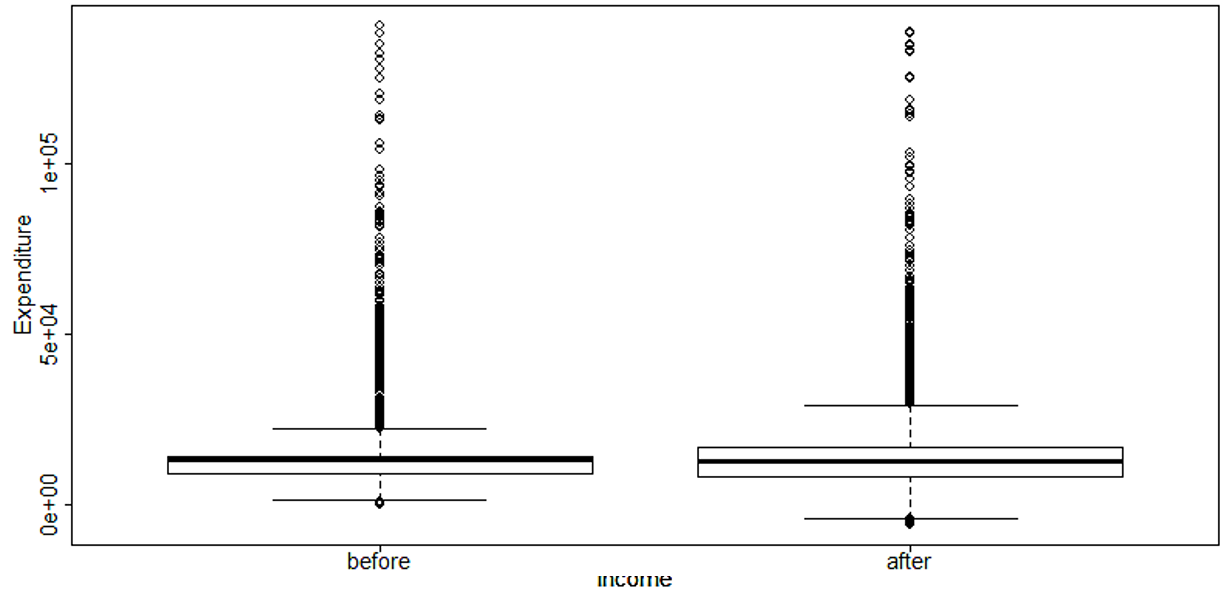
(#fig:fig5_sec05)Ejemplo de diagramas de caja de una variable de gasto antes y después de la anonimización.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.89.
9.2.0.3 Gráficos de mosaico
Los gráficos de mosaico univariados y multivariados son útiles para mostrar cambios en las tabulaciones de variables categóricas, especialmente cuando se comparan varios “escenarios” uno al lado del otro. Un escenario aquí se refiere a la elección de métodos de anonimización y sus parámetros. Con gráficos de mosaico podemos, por ejemplo, ver rápidamente el efecto de diferentes niveles de k-anonimato o diferencias en los vectores de importancia en el algoritmo de supresión local (ver la Sección Supresión local.
Ilustramos los cambios en las tabulaciones con un ejemplo de la variable “WATER” antes y después de aplicar PRAM. Podemos usar gráficos de mosaico para ver rápidamente los cambios de cada categoría. El Bloque 9.13 muestra el código en R . La función mosaicplot() está disponible en el paquete base de R. Para graficar una tabulación, primero se debe hacer la tabulación con la función table(). Para mostrar las etiquetas en mosaicplot(), cambiamos la clase de las variables a ‘factor’. Al observar el gráfico de mosaico en la Figura @ref(fig:fig6_sec05), vemos que la PRAM invariante prácticamente no tiene influencia en la distribución univariante.
Bloque 9.13 Creando mosaicos univariados
# Recopilación de datos de la variable WATER antes y después de la anonimización
# asignación de etiquetas al gráfico
dataWater <- t(cbind(table(factor(sdcHH@origData$WATER,
levels = c(1, 2, 3, 4, 5, 6, 7, 8, 9),
labels = c("Pipe (own tap)", "Public standpipe",
"Borehole", "Wells (protected)",
"Wells (unprotected)", "Surface water",
"Rain water", "Vendor/truck", "Other"))),
table(factor(sdcHH@manipPramVars$WATER,
levels = c(1,2, 3, 4, 5, 6, 7, 8, 9),
labels = c("Pipe (own tap)", "Public standpipe",
"Borehole", "Wells (protected)",
"Wells (unprotected)", "Surface water",
"Rain water", "Vendor/truck","Other")))))
rownames(dataWater) <- c("before", "after")
# gráfico de mosaico
mosaicplot(dataWater, main = "", color = 2:10, las = 2)
(#fig:fig6_sec05)Gráfico de mosaico para ilustrar los cambios en la variable WATER.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.90.
Usamos las variables “gender” y “relationship status” para ilustrar el uso de gráficos de mosaico para la ilustración de cambios en las tabulaciones univariadas introducidas por varios conjuntos de métodos de anonimización. La Tabla 9.1 proporciona los métodos aplicados en cada escenario. El escenario 0, el escenario base, muestra las categorías originales de las variables de género y estado civil, mientras que los escenarios 1 a 6 muestran cambios en las categorías después de aplicar diferentes técnicas de anonimización. La tabla muestra una descripción de los métodos de anonimización utilizados en cada escenario. En total, visualizamos el impacto de seis conjuntos diferentes de métodos de anonimización. Podemos usar gráficos de mosaico para ver rápidamente qué conjunto de métodos tiene qué impacto en las variables de gender y relationship status, que se pueden usar para seleccionar el mejor escenario. Mirando los gráficos de mosaico en la Figura @ref(fig:fig7_sec05), vemos que los escenarios 2, 5 y 6 dan los cambios más pequeños para la variable de gender y los escenarios 3 y 4 para la variable de relationship status.
| Escenario | Descripción de los métodos de anonimización aplicados |
|---|---|
| 0 (base) | Datos originales sin tratamiento |
| 1 | Recodificar age (intervalos de cinco años), más la supresión local (requerido k = 3, alta importancia en las variables de water, toilet y literacy) |
| 2 | Recodificar age (intervalos de cinco años), más supresión local (requerido k = 5, sin vector de importancia) |
| 3 | Recodificar la age (intervalos de cinco años), más la supresión local (requerido k = 3, alta importancia en toilet), al mismo tiempo que se recodifican las variables region, urban, education level y ocupation |
| 4 | Recodificar age (pasos de cinco años), más supresión local (requerido k = 5, alta importancia en water, toilet, y education level), al mismo tiempo que se recodifican variables de region, urban, education level y ocupation |
| 5 | Recodificar age (intervalos de cinco años), más supresión local (requerido k = 3, sin vector de importancia), microagregación (wealth index), al mismo tiempo que se recodifican variables de region, urban, education level y ocupation |
| 6 | Recodificar age (intervalos de cinco años) más supresión local (requerido k=3, sin vector de importancia), literacy PRAM, al mismo tiempo que se recodifican variables de region, urban, education level y ocupation |
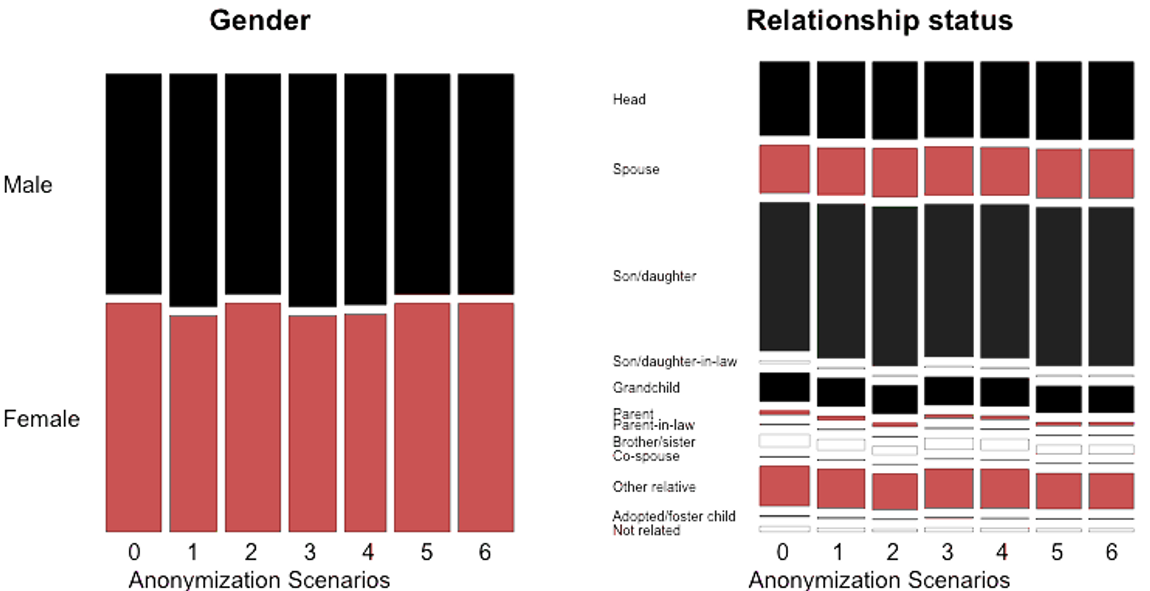
(#fig:fig7_sec05)Comparación de variables de gender y relationship status tratadas versus no tratadas con gráficos de mosaico.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.91
PRAM preserva las distribuciones univariadas. Por lo tanto, en este caso es más interesante observar los gráficos de mosaico multivariado. Los diagramas de mosaico también son una herramienta poderosa para mostrar cambios en tabulaciones cruzadas/tablas de contingencia. El Bloque 9.14 a continuación muestra cómo generar gráficos de mosaico para dos variables. Para comparar los cambios, necesitamos comparar dos gráficos diferentes. La Figura @ref(fig:fig8_sec05) y la Figura @ref(fig:fig9_sec05) ilustran que la PRAM no conserva las tablas de doble entrada en este caso.
Bloque 9.14 Creando mosaicos multivariados
# Antes de la anonimización: tabla de contingencia y gráfico de mosaico
ROOFTOILETbefore <- t(table(factor(sdcHH@origData$ROOF, levels = c(1,2, 3, 4, 5, 9),
labels = c("Concrete/cement/ \n brick/stone", "Wood",
"Bamboo/thatch", "Tiles/shingles",
"Tin/metal sheets", "Other")),
factor(sdcHH@origData$TOILET, levels = c(1,2, 3, 4, 9),
labels = c("Flush \n toilet",
"Improved \n pit \n latrine",
"Pit \n latrine", "No \n facility",
"Other"))))
mosaicplot(ROOFTOILETbefore, main = "", las = 2, color = 2:6)
# Después de la anonimización: tabla de contingencia y gráfico de mosaico
ROOFTOILETafter <- t(table(factor(sdcHH@manipPramVars$ROOF, levels = c(1,2, 3, 4, 5, 9),
labels = c("Concrete/cement/ \n brick/stone", "Wood",
"Bamboo/thatch", "Tiles/shingles",
"Tin/metal sheets", "Other")),
factor(sdcHH@manipPramVars$TOILET, levels = c(1,2, 3, 4, 9),
labels = c("Flush \n toilet",
"Improved \\n pit \n latrine",
"Pit \n latrine", "No \n facility",
"Other"))))
mosaicplot(ROOFTOILETafter, main = "", las = 2, color = 2:6)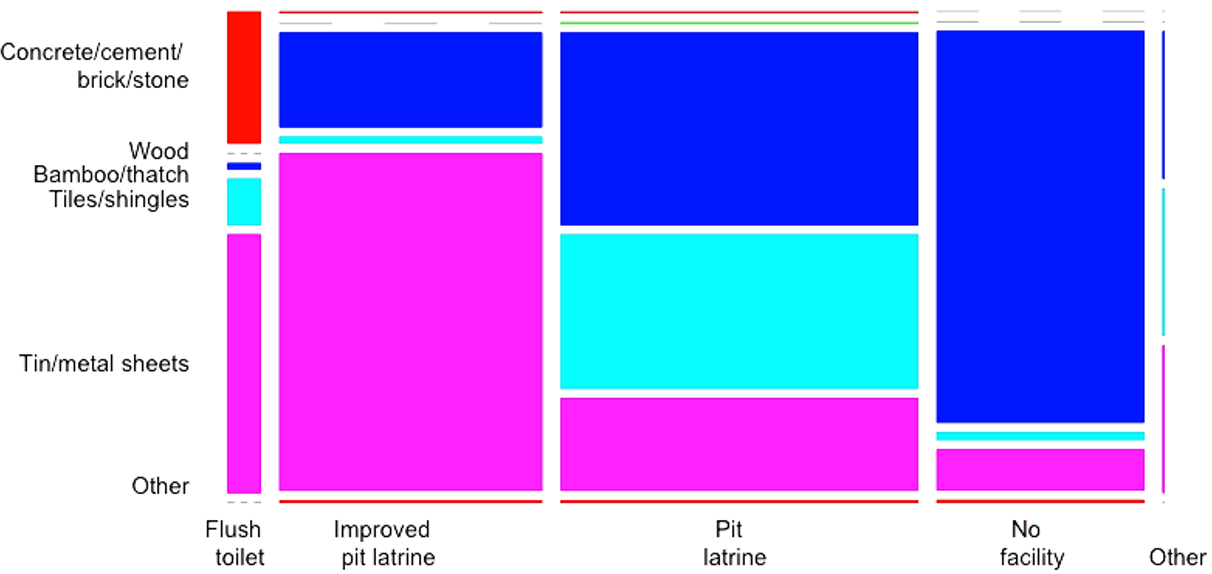
(#fig:fig8_sec05)Gráfico de mosaico de las variables ROOF e TOILET antes de la anonimización.
Fuente: Imagen extraída de (Benschop and Welch 2021),pág. 92.
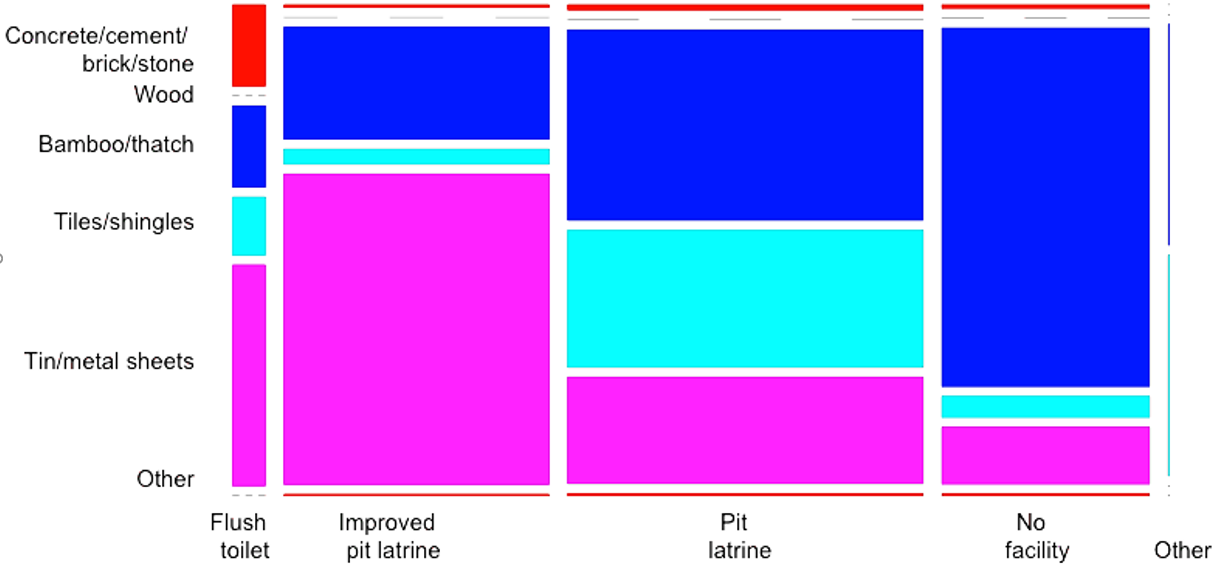
(#fig:fig9_sec05)Gráfico de mosaico de las variables ROOF e TOILET después de la anonimización.
Fuente: Imagen extraída de (Benschop and Welch 2021), pág.93.
9.2.1 Elección de la medida de utilidad
Además de los requisitos de los usuarios sobre los datos, las medidas de utilidad deben elegirse de acuerdo con los tipos de variables y los métodos de anonimización empleados. Las medidas de utilidad empleadas pueden ser una combinación de medidas generales y específicas del usuario. Como se discutió anteriormente, se deben usar diferentes medidas de utilidad para datos continuos y categóricos. Además, algunas medidas de utilidad no son informativas después de que se hayan aplicado ciertos métodos de anonimización. Por ejemplo, después de aplicar métodos perturbativos que intercambian valores de datos, la comparación directa de valores no es útil porque dará la impresión de altos niveles de pérdida de información. En tales casos, es más informativo observar las medias, las covarianzas y los indicadores de evaluación comparativa que se pueden calcular a partir de los datos. Es más, es importante no solo centrarse en las características de las variables una por una, sino también en las interacciones entre las variables. Esto se puede hacer mediante tabulaciones cruzadas y regresiones. En general, al anonimizar datos muestreados, es recomendable calcular intervalos de confianza alrededor de las estimaciones para interpretar la magnitud de los cambios.
Nota: Para material de lectura recomendado sobre la medición de la utilidad y la pérdida de información ver (De Waal and Willenborg 1999), (J. Domingo-Ferrer and Torra 2001) y (J. Domingo-Ferrer and Torra 2001).
Referencias
Es posible liberar archivos de datos para diferentes grupos de usuarios, por ejemplo, PUF y SUF. Sin embargo, toda la información en el archivo menos detallado también debe incluirse en el archivo más detallado para evitar la divulgación no deseada. Los conjuntos de datos publicados en enclaves de datos se pueden personalizar para el usuario, ya que el riesgo de que se combinen con otra versión es cero.↩︎
Aquí, el objeto
sdcMicro“sdcIntial” contiene un conjunto de datos con 2500 personas y 103 variables. Seleccionamos cuatro cuasi-identificadores categóricos: “URBRUR”, “REGION”, “RELIG” y “MARITAL” y varios cuasi-identificadores continuos relativos a ingresos y gastos. Para ilustrar la pérdida de utilidad, también aplicamos varios métodos SDC a este objetosdcMicro, como supresión local, PRAM y adición de ruido aditivo.↩︎