Capítulo 7 Medición de riesgos

7.1 Tipos de divulgación

Medir el riesgo de divulgación es una parte importante del proceso SDC: las medidas de riesgo se utilizan para juzgar si un archivo de datos es lo suficientemente seguro para su liberación. Antes de medir el riesgo de divulgación, debemos definir qué tipo de divulgación es relevante para los datos disponibles, a saber: divulgación de identidad, divulgación de atributos y divulgación inferencial (ver Lambert (1993) y Anco Hundepool et al. (2012)).

  • Divulgación de identidad, que ocurre si el intruso asocia a un individuo conocido con un registro de datos publicado. Por ejemplo, el intruso vincula un registro de datos publicado con información externa o identifica a un informante con valores de datos extremos. En este caso, un intruso puede explotar un pequeño subconjunto de variables para realizar la vinculación, y una vez que la vinculación es exitosa, el intruso tiene acceso a toda la demás información en los datos publicados relacionados con el informante específico.

  • Divulgación de atributos, que ocurre si el intruso puede determinar algunas características nuevas de un individuo en función de la información disponible en los datos publicados. La divulgación de atributos ocurre si se vuelve a identificar correctamente a un informante y el conjunto de datos incluye variables que contienen información que el intruso desconocía previamente. La divulgación de atributos también puede ocurrir sin divulgación de identidad. Por ejemplo, si un hospital publica datos que muestran que todas las pacientes de 56 a 60 años que tienen cáncer, un intruso conoce la condición médica de cualquier paciente de 56 a 60 años en el conjunto de datos sin tener que identificar a la persona específica.

  • Divulgación inferencial, que ocurre si el intruso es capaz de determinar el valor de alguna característica de un individuo con mayor precisión con los datos liberados de lo que hubiera sido posible de otro modo. Por ejemplo, con un modelo de regresión altamente predictivo, un intruso puede inferir la información confidencial de ingresos de un informante utilizando atributos registrados en los datos, lo que lleva a una divulgación inferencial.

Los métodos SDC para microdatos están destinados a evitar la divulgación de identidades y atributos. La divulgación inferencial generalmente no se aborda en SDC en el entorno de microdatos, ya que los microdatos se liberan precisamente para que los investigadores puedan hacer inferencias estadísticas y comprender las relaciones entre las variables. En ese sentido, la inferencia no puede compararse con la divulgación. Además, las inferencias están diseñadas para predecir el comportamiento agregado, no individual y, por lo tanto, suelen ser malos predictores de valores de datos individuales.

7.2 Clasificación de variables

A los efectos del proceso SDC, utilizamos las clasificaciones de variables descritas en los siguientes párrafos (consulte la Figura 7.1 para obtener una descripción general). La clasificación inicial de variables en variables de identificación y no identificación depende de la forma en que los intrusos pueden utilizar las variables para la reidentificación:

  • Variables de identificación: contienen información que puede conducir a la identificación de los informantes y se pueden clasificar en:

    • Los identificadores directos, que revelan de manera directa e inequívoca la identidad del informante. Algunos ejemplos son nombres, números de pasaporte, números de identificación social y direcciones. Los identificadores directos deben eliminarse del conjunto de datos antes de su publicación. La eliminación de identificadores directos es un proceso sencillo y siempre es el primer paso para producir un conjunto de microdatos seguro para su publicación. Sin embargo, la eliminación de identificadores directos a menudo no es suficiente.

    • Los identificadores indirectos (cuasi-identificadores o variables clave) contienen información que, cuando se combina con otros identificadores indirectos en el conjunto de datos, puede conducir a la reidentificación de los informantes. Este es especialmente el caso cuando se pueden usar para hacer coincidir la información con otra información o datos externos. Ejemplos de identificadores indirectos son la raza, la fecha de nacimiento, el sexo y el código postal, que pueden combinarse o vincularse fácilmente con información externa disponible públicamente y hacer posible la identificación. Las combinaciones de valores de varios identificadores indirectos se denominan claves. Los valores de los identificadores indirectos por sí mismos a menudo no conducen a la identificación (por ejemplo, hombre/mujer), pero una combinación de varios valores de identificador indirecto puede hacer que un registro sea único (por ejemplo, hombre, 18 años, casado) y, por lo tanto, identificable. En general, no es aconsejable eliminar simplemente los identificadores indirectos de los datos para resolver el problema. En muchos casos, serán variables importantes para cualquier análisis sensato. En la práctica, cualquier variable en el conjunto de datos podría potencialmente usarse como un identificador indirecto. SDC aborda esto mediante la identificación de variables como identificadores indirectos y anonimizándolas mientras mantiene la información en el conjunto de datos para su publicación.

  • Las variables de no identificación son variables que no se pueden utilizar para volver a identificar a los informantes. Esto podría deberse a que estas variables no están contenidas en ningún otro archivo de datos u otras fuentes externas y no son observables por un intruso. No obstante, las variables de no identificación son importantes en el proceso SDC, ya que pueden contener información confidencial/sensible, que puede resultar perjudicial si se produce una divulgación como resultado de la divulgación de la identidad basada en variables de identificación.

Estas clasificaciones de variables dependen parcialmente de la disponibilidad de conjuntos de datos externos que pueden contener información que, cuando se combina con los datos actuales, podría conducir a la divulgación. La identificación y clasificación de variables como identificadores indirectos depende, entre otros, de la disponibilidad de información en conjuntos de datos externos. Un paso importante en el proceso SDC es definir una lista de posibles escenarios de divulgación en función de cómo los identificadores indirectos podrían combinarse entre sí y la información en conjuntos de datos externos, y luego tratar los datos para evitar la divulgación. Analizamos los escenarios de divulgación con más detalle en la sección Escenarios de divulgación.

Para el proceso SDC, también es útil clasificar aún más los identificadores indirectos en variables categóricas, continuas y semicontinuas o discretas. Esta clasificación es importante para determinar los métodos SDC apropiados para esa variable, así como la validez de las medidas de riesgo.

  • Las variables categóricas toman valores sobre un conjunto finito, y cualquier operación aritmética que las utilice generalmente no tiene sentido o no está permitida. Ejemplos de variables categóricas son género, región y nivel educativo.

  • Las variables continuas pueden tomar un número infinito de valores en un conjunto denso. Algunos ejemplos son los ingresos, la altura del cuerpo y el tamaño del terreno. Las variables continuas se pueden transformar en variables categóricas mediante la construcción de intervalos (como bandas de ingresos)12.

  • Las variables semicontinuas o discretas son variables continuas que toman valores limitados a un conjunto finito. Un ejemplo es la edad medida en años, que podría tomar valores en el conjunto {0, 1,…, 100}. La naturaleza finita de los valores de estas variables significa que pueden tratarse como variables categóricas a los efectos de SDC 13.

Además de estas clasificaciones de variables, el proceso SDC clasifica aún más las variables según su sensibilidad o confidencialidad. Tanto las variables identificadoras indirectas como las de no identificación pueden clasificarse como sensibles (o confidenciales) o no sensibles (o no confidenciales). Esta distinción no es importante para los identificadores directos, ya que los identificadores directos se eliminan de los datos publicados.

  • Las variables sensibles contienen información confidencial que no debe liberarse sin un tratamiento adecuado, utilizando los métodos de SDC para reducir el riesgo de divulgación. Algunos ejemplos son los ingresos, la religión, la afiliación política y las variables relativas a la salud. Que una variable sea sensible depende del contexto y del país: una determinada variable puede considerarse sensible en un país y no sensible en otro.

  • Las variables no sensibles contienen información no confidencial sobre el informante, como el lugar de residencia o el área de residencia rural/urbana. Sin embargo, la clasificación de una variable como no sensible no significa que no deba ser considerada en el proceso de SDC. Las variables no sensibles aún pueden servir como identificadores indirectos cuando se combinan con otras variables u otros datos externos.

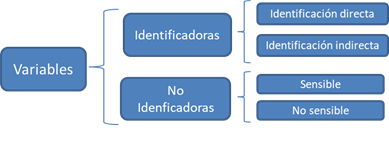
Clasificación de las variables.

Figura 7.1: Clasificación de las variables.

7.3 Escenarios de divulgación

La evaluación del riesgo de divulgación se lleva a cabo con referencia a las fuentes de datos disponibles en el entorno donde se liberará el conjunto de datos. En este contexto, el riesgo de divulgación es la posibilidad de volver a identificar correctamente a una unidad en el archivo de microdatos publicado 14 comparando sus datos con un archivo externo basado en un conjunto de identificadores indirectos. La evaluación de riesgos se realiza mediante la identificación de los llamados escenarios de divulgación o intrusión. Un escenario de divulgación describe la información potencialmente disponible para el intruso (por ejemplo, datos del censo, padrones electorales, registros de población o datos recopilados por empresas privadas) para identificar a los informantes y las formas en que dicha información puede combinarse con el conjunto de microdatos que se liberará y utilizará para reidentificación de registros en el conjunto de datos. Normalmente, estos conjuntos de datos externos incluyen identificadores directos. En ese caso, la reidentificación de los registros en el conjunto de datos publicado conduce a la divulgación de la identidad y, posiblemente, de los atributos. El principal resultado de la evaluación de los escenarios de divulgación es la identificación de un conjunto de identificadores indirectos (es decir, variables clave) que deben tratarse durante el proceso SDC (ver Elliot et al. (2010)).

Un ejemplo de un escenario de divulgación podría ser el reconocimiento espontáneo de un informante por parte de un investigador. Por ejemplo, mientras revisa los datos, el investigador reconoce a una persona con una combinación inusual de las variables edad y estado civil. Por supuesto, esto solo puede suceder si la persona es bien conocida o es conocida por el investigador. Otro ejemplo de un escenario de divulgación para un archivo disponible públicamente sería si las variables en los datos pudieran vincularse a un registro electoral disponible públicamente. Un intruso podría hacer coincidir todo el conjunto de datos con las personas del registro. Sin embargo, esto puede ser difícil y requerir experiencia especializada, o software, y se deben cumplir otras condiciones. Los ejemplos son que el momento en el que se recopilaron los conjuntos de datos debe coincidir aproximadamente y el contenido de las variables debe ser (casi) idéntico. Si no se cumplen estas condiciones, la coincidencia exacta es mucho menos probable.

La evaluación del riesgo de divulgación se basa en los identificadores indirectos, que se identifican en el análisis de escenarios de riesgo de divulgación. El riesgo de divulgación depende directamente de la inclusión o exclusión de variables en el conjunto de identificadores indirectos elegidos. Por lo tanto, este paso en el proceso SDC (hacer la elección de los identificadores indirectos) debe abordarse con gran reflexión y cuidado. Veremos más adelante, cuando discutamos los pasos en el proceso de SDC con más detalle, que el primer paso para cualquier oficina de estadística es realizar un ejercicio en el que se compila un inventario de todos los conjuntos de datos disponibles en el país. Se consideran tanto los conjuntos de datos publicados por la oficina nacional de estadística (como el INE) como por otras fuentes y se analiza su disponibilidad para los intrusos, así como las variables incluidas en estos conjuntos de datos.

7.4 Niveles de riesgo

Con microdatos de encuestas y censos, a menudo tenemos que preocuparnos por la divulgación a nivel individual o de unidad, es decir, identificar a los informantes individuales. Los informantes individuales suelen ser personas físicas, pero también pueden ser unidades, como empresas, escuelas, centros de salud, etc. Los archivos de microdatos suelen tener una estructura jerárquica en la que las unidades individuales pertenecen a grupos, por ejemplo, las personas pertenecen a hogares. La estructura jerárquica más común en los microdatos es la estructura del hogar en los datos de las encuestas de hogares. Por lo tanto, en esta guía, a veces llamamos al riesgo de divulgación de datos con una estructura jerárquica “riesgo hogar”. Sin embargo, los conceptos se aplican por igual a los datos del establecimiento y otros datos con estructuras jerárquicas, como los datos de la escuela con los alumnos y profesores o los datos de la empresa con los empleados.

Veremos que es importante tener en cuenta esta estructura jerárquica al medir el riesgo de divulgación. Para los datos jerárquicos, la información recopilada en el nivel jerárquico superior (por ejemplo, nivel del hogar) sería la misma para todos los individuos del grupo que pertenecen a ese nivel jerárquico superior (por ejemplo, el hogar) [Los supuestos para esta medida de riesgo son estrictos y el riesgo se estima en muchos casos mayor que el riesgo real. Entre otras suposiciones, se supone que todos los individuos de la muestra también están incluidos en el archivo externo utilizado por el intruso para compararlos. Si no es así, el riesgo es mucho menor; si el individuo en el archivo liberado no está incluido en el archivo externo, la probabilidad de una coincidencia correcta es cero. Otras suposiciones son que los archivos no contienen errores y que ambos conjuntos de datos se recopilaron simultáneamente, es decir, contienen la misma información. Estos supuestos a menudo no se cumplen en general, pero son necesarios para el cálculo de una medida. Un ejemplo de una violación de las últimas suposiciones podría ocurrir si los conjuntos de datos se recopilan en diferentes puntos en el tiempo y los registros han cambiado. Esto podría suceder cuando las personas se mudan o cambian de trabajo y hace imposible la coincidencia correcta. Los supuestos son conservadores y asumen el mayor riesgo de divulgación.]. Algunos ejemplos típicos de variables que tendrían los mismos valores para todos los miembros de una misma unidad jerárquica superior son, en el caso de los hogares, las relativas a la vivienda y los ingresos del hogar. Estas variables difieren de una encuesta a otra y de un país a otro 15. Esta estructura jerárquica crea un mayor nivel de riesgo de divulgación por dos razones:

  1. si se reidentifica a una persona del hogar, la estructura del hogar permite la reidentificación de los demás miembros del hogar en el mismo hogar,

  2. los valores de las variables para otros miembros del hogar que son comunes para todos los miembros del hogar pueden usarse para volver a identificar a otro individuo del mismo hogar. Esto se analiza con más detalle en la sección Riesgo jerárquico (o del hogar).

A continuación, primero analizamos las medidas de riesgo utilizadas para evaluar el riesgo de divulgación en ausencia de una estructura jerárquica. Esto incluye medidas de riesgo que buscan agregar el riesgo individual para todos los individuos en el archivo de microdatos; el objetivo es cuantificar una medida de riesgo de divulgación global para el archivo. Luego discutimos cómo cambian las medidas de riesgo cuando se tiene en cuenta la estructura jerárquica de los datos.

También discutiremos cómo las medidas de riesgo difieren para los identificadores indirectos categóricos y continuos. Para las variables categóricas, utilizaremos el concepto de unicidad de combinaciones de valores de identificadores indirectos (las llamadas “claves”) que se utilizan para identificar a las personas en riesgo. El concepto de unicidad, sin embargo, no es útil para variables continuas, ya que es probable que todos o muchos individuos tengan valores únicos para esa variable, por definición de una variable continua. Las medidas de riesgo para variables categóricas son generalmente medidas a priori, es decir, pueden evaluarse antes de aplicar métodos de anonimización ya que se basan en el principio de unicidad. Las medidas de riesgo para variables continuas son medidas a posteriori; se basan en la comparación de los microdatos antes y después de la anonimización y son, por ejemplo, basadas en la proximidad de observaciones entre conjuntos de datos originales y tratados (anonimizados).

Los archivos que se limitan solo a identificadores indirectos categóricos o continuos son los más fáciles para medir el riesgo. Veremos en secciones posteriores que, en los casos en que ambos tipos de variables están presentes, la recodificación de variables continuas en categorías es un enfoque para simplificar el proceso SDC, pero también veremos que desde una perspectiva de utilidad esto puede no ser deseable. Un ejemplo podría ser el uso de quintiles de ingresos en lugar de las variables de ingresos reales. Veremos que medir el riesgo de divulgación con base en las variables categóricas y continuas por separado generalmente no es un enfoque válido.

Las medidas de riesgo discutidas en la siguiente sección se basan en varios supuestos. En general, estas medidas se basan en suposiciones bastante restrictivas y, a menudo, conducirán a estimaciones de riesgo conservadoras. Estas medidas de riesgo conservadoras pueden exagerar el riesgo ya que suponen el peor de los casos. Sin embargo, se deben cumplir dos suposiciones para que las medidas de riesgo sean válidas y significativas; los microdatos deben ser una muestra de una población más grande (no censo) y las ponderaciones de la muestra deben estar disponibles.

7.5 Riesgo individual

7.5.1 Identificadores indirectos categóricos y recuentos de frecuencia

El enfoque principal de la medición del riesgo para los identificadores indirectos categóricos es la divulgación de la identidad. La medición del riesgo de divulgación se basa en la evaluación de la probabilidad de reidentificación correcta de las personas en los datos publicados. Utilizamos medidas basadas en los microdatos reales que se publicarán. En general, cuanto más rara sea la combinación de valores de los identificadores indirectos (es decir, clave) de una observación en la muestra, mayor será el riesgo de revelación de identidad. Un intruso que intente hacer coincidir a una persona que tiene una clave relativamente rara dentro de los datos de muestra con un conjunto de datos externo en el que existe la misma clave tendrá una mayor probabilidad de encontrar una coincidencia correcta que cuando un número mayor de personas comparten la misma clave. Esto se puede ilustrar con el siguiente ejemplo que se ilustra en la Tabla 7.1.

La Tabla 7.1 muestra los valores de 10 informantes para los identificadores indirectos “área”, “género”, “nivel educacional” y “situación laboral”. En los datos, encontramos siete combinaciones únicas de valores de identificadores indirectos (es decir, patrones o claves) de los cuatro identificadores indirectos. Ejemplos de claves son {‘urbano’, ‘femenino’, ‘secundaria incompleta’, ‘ocupado’} y {‘urbano’, ‘femenino’, ‘primaria incompleta’, ‘no FL’}. Sea \(f_{k}\) la frecuencia de muestreo de la k-ésima clave, es decir, el número de individuos de la muestra con valores de los identificadores indirectos que coinciden con la clave k. Este sería 2 para la clave {urbano, femenino, secundaria incompleta, ocupado}, ya que esta clave es compartida por los individuos 1 y 2 y 1 para la clave {‘urbano’, ‘femenino’, ‘primaria incompleta’, ‘no FL’}, que es exclusivo del individuo 3. Por definición, \(f_{k}\) es el mismo para cada registro que comparte una clave particular.

Tabla 7.1: Conjunto de datos de ejemplo que muestra frecuencias de muestra, frecuencias de población y riesgo de divulgación individual
Id Área Género Nivel educacional Situación laboral Peso (\(w_{i}\)) \(f_{k}\) \(F_{k}\) Riesgo (\(r_{k}\))
1 Urbano Femenino Secundaria incompleta Ocupado 180 2 360 0.0054
2 Urbano Femenino Secundaria incompleta Ocupado 180 2 360 0.0054
3 Urbano Femenino Primaria incompleta No FL 215 1 215 0.0251
4 Urbano Masculino Secundaria completa Ocupado 76 2 152 0.0126
5 Rural Femenino Secundaria completa Desocupado 186 1 186 0.0282
6 Urbano Masculino Secundaria completa Ocupado 76 2 152 0.0126
7 Urbano Femenino Primaria completa No FL 180 1 180 0.029
8 Urbano Masculino Post secundaria Desocupado 215 1 215 0.0251
9 Urbano Femenino Secundaria incompleta No FL 186 2 262 0.0074
10 Urbano Femenino Secundaria incompleta No FL 76 2 262 0.0074

Fuente: Adaptación de (Benschop, Machingauta, and Welch 2021, 28)

Cuanto menos personas con las que una persona comparte su combinación de identificadores indirectos, más probable es que la persona coincida correctamente en otro conjunto de datos que contenga estos identificadores indirectos. Incluso cuando los identificadores directos se eliminan del conjunto de datos, esa persona tiene un mayor riesgo de divulgación que otras, suponiendo que sus pesos de muestra sean los mismos. La Tabla 7.1 reporta las frecuencias de muestreo \(f_{k}\) de las llaves para todos los individuos. Las personas con las mismas claves tienen la misma frecuencia de muestreo. Si \(f_{k}=1\), este individuo tiene una combinación única de valores de identificadores indirectos y se denomina “muestra única”. El conjunto de datos de la Tabla 7.1 contiene cuatro muestras únicas. Las medidas de riesgo se basan en esta frecuencia de muestreo.

En el Bloque 7.1, mostramos cómo usar el paquete sdcMicro para crear una lista de frecuencias de muestra \(f_{k}\) para cada registro en un conjunto de datos. Esto se hace usando la función sdcMicro freq(). Un valor de 2 para una observación significa que en la muestra hay un individuo más con exactamente la misma combinación de valores para los identificadores indirectos seleccionados. En el Bloque 7.1, la función freq() se aplica a “sdcInitial”, que es un objeto sdcMicro. Los objetos se usan cuando se hace SDC con sdcMicro. La función freq() muestra la frecuencia de muestreo de las claves construidas sobre un conjunto definido de identificadores indirectos. El Bloque 7.1 corresponde a los datos de la Tabla 7.1.

Bloque 7.1 Cálculo \(f_{k}\) usando sdcMicro

setwd("..\Capacitación\GitHub") # directorio de trabajo

library(sdcMicro) # carga paquete sdcMicro
# Set up conjunto de datos
data <- as.data.frame(cbind(as.factor(c('Urbano', 'Urbano', 'Urbano', 'Urbano',
                                        'Rural', 'Urbano', 'Urbano', 'Urbano',
                                        'Urbano', 'Urbano')),
                            as.factor(c('Femenino', 'Femenino', 'Femenino',
                                        'Masculino','Femenino', 'Masculino',
                                        'Femenino', 'Masculino', 'Femenino',
                                        'Femenino')),
                            as.factor(c('Sec in', 'Sec in', 'Prim in', 'Sec com',
                                        'Sec com', 'Sec com', 'Prim com', 'Post-sec',
                                        'Sec in', 'Sec in')),
                            as.factor(c('Ocu', 'Ocu', 'No-FL', 'Ocu', 'Desocu', 'Ocu',
                                        'No-FL', 'Desocu', 'No-FL','No-FL')),
                            as.factor(c('Sí', 'Sí', 'Sí', 'Sí', 'Sí', 'No', 'No',
                                        'Sí', 'No', 'Sí')),
                            c(180, 180, 215, 76, 186, 76, 180, 215, 186, 76)
))

# Especificar nombres de variables
names(data) <- c('Área', 'Género', 'Educ', 'SitLab', 'Salud', 'Pesos')               

# Set up objeto sdcMicro con especificación de identificadores indirectos y pesos
sdcInitial <- createSdcObj(dat = data, keyVars = c('Área', 'Género', 'Educ', 'SitLab'),
                           weightVar = 'Pesos')
data$fk<-freq(sdcInitial, type = 'fk')

Para datos de muestra, es más interesante mirar \(F_{k}\), la frecuencia de población de una combinación de identificadores indirectos (clave) k, que es el número de individuos de la población con la clave que corresponde a la clave k. Se desconoce la frecuencia poblacional si los microdatos son una muestra y no un censo. Bajo ciertas suposiciones, el valor esperado de las frecuencias de la población se puede calcular utilizando el peso del diseño de la muestra \(w_{i}\)(en una muestra simple, esta es la inversa de la probabilidad de inclusión) para cada individuo i.

\[F_{k}=\sum_{i|individuo\,i\, correspondiente\, a\, la\, clave\, k} w_{i}\]

\(F_{k}\) es la suma de los pesos muestrales de todos los registros con la misma clave k. Por lo tanto, como \(f_{k}\), \(F_{k}\) es el mismo para cada registro con clave k. El riesgo de una reidentificación correcta es la probabilidad de que la clave coincida con el individuo correcto de la población. Dado que cada individuo en la muestra con clave k corresponde a \(F_{k}\) individuos en la población, la probabilidad de reidentificación correcta es \(1/F_{k}\). Esta es la probabilidad de reidentificación en el peor de los casos y puede interpretarse como riesgo de divulgación. Los individuos con la misma clave tienen las mismas frecuencias, es decir, la frecuencia de la clave.

Si \(F_{k}=1\), la clave k es tanto una muestra como una población única y el riesgo de divulgación sería 1. Las características únicas de la población son un factor importante a considerar al evaluar el riesgo y merecen especial atención.

Además, \(f_{k}\), la frecuencia de muestreo de la clave k (es decir, el número de individuos en la muestra con la combinación de identificadores indirectos correspondientes a la combinación especificada en la clave k) y \(F_{k}\), la frecuencia de población estimada de k, se puede visualizar en sdcMicro. El Bloque 7.2 ilustra cómo devolver listas de longitud n de frecuencias para todos los individuos. Las frecuencias se muestran para cada individuo y no para cada clave.

Bloque 7.2 Cálculo de frecuencias muestrales y poblacionales usando sdcMicro

# frecuencia muestral de individuos
data$fk<-freq(sdcInitial, type = 'fk')
# frecuencia poblacional de individuos
data$FK<-freq(sdcInitial, type = 'Fk')

En la práctica, este enfoque conduce a estimaciones de riesgo conservadoras, ya que no tiene en cuenta adecuadamente los métodos de muestreo. En este caso, las estimaciones del riesgo de reidentificación pueden ser demasiado altas. Si se utiliza este riesgo sobreestimado, los datos pueden estar sobreprotegidos (es decir, la pérdida de información será mayor que la necesaria) al aplicar las medidas de SDC.

La medida del riesgo \(r_{k}\) es como \(f_{k}\) y \(F_{k}\), el mismo para todos los individuos que comparten el mismo patrón de valores de identificadores indirectos y se denomina riesgo individual. Los valores \(r_{k}\) también puede interpretarse como la probabilidad de divulgación de los individuos o como la probabilidad de una coincidencia exitosa con individuos elegidos al azar de un archivo de datos externo con los mismos valores de los identificadores indirectos. Esta medida de riesgo se basa en ciertos supuestos 16, que son estrictos y pueden conducir a una medida de riesgo relativamente conservadora. En sdcMicro, la medida de riesgo \(r_{k}\) se calcula automáticamente al crear un objeto sdcMicro y se guarda en el slot de “riesgo” 17. El Bloque 7.3 muestra cómo recuperar las medidas de riesgo usando sdcMicro para nuestro ejemplo. Las medidas de riesgo también se presentan en la Tabla 7.1.

Bloque 7.3 Slot de riesgo individual en el objeto sdcMicro

sdcInitial@risk$individual

Los principales factores que influyen en el riesgo individual son las frecuencias de muestreo \(f_{k}\) y los pesos de diseño de muestreo \(w_{i}\). Si un individuo tiene un riesgo relativamente alto de divulgación, en nuestro ejemplo serían los individuos 3, 5, 7 y 8 en la Tabla 7.1 y el Bloque 7.3, la probabilidad de que un posible intruso relacione correctamente a estos individuos con un archivo de datos externo es relativamente alta. En nuestro ejemplo, la razón del alto riesgo es el hecho de que estos individuos son muestras únicas (es decir, \(f_{k}=1\)). Este riesgo es el riesgo del peor de los casos y no implica que la persona sea reidentificada con certeza con esta probabilidad. Por ejemplo, si un individuo incluido en los microdatos no está incluido en el archivo de datos externo, la probabilidad de una coincidencia correcta es cero. No obstante, la medida del riesgo calculada a partir de las frecuencias será positiva como medida de evaluación.

7.5.2 k-anonimato

La medida del riesgo k- anonimato se basa en el principio de que, en un conjunto de datos seguro, el número de personas que comparten la misma combinación de valores (claves) de identificadores indirectos categóricos debe ser superior a un umbral especificado k. El k-anonimato es una medida de riesgo basada en los microdatos a publicar, ya que solo tiene en cuenta la muestra. Un individuo viola el k-anonimato si la frecuencia de muestreo \(f_{k}\) para la llave k es menor que el umbral especificado k. Por ejemplo, si un individuo tiene la misma combinación de identificadores indirectos que otros dos individuos en la muestra, estos individuos satisfacen el 3-anonimato pero violan el 4-anonimato. En el conjunto de datos de la Tabla 7.1, seis personas satisfacen el 2-anonimato y cuatro violan el 2-anonimato. Los individuos que violan el 2-anonimato son muestras únicas. La medida de riesgo es el número de observaciones que violan el k-anonimato para un cierto valor de k, que es

\[ \sum_{i} I(f_{k}<k), \]

donde \(I\) es la función indicadora e \(i\) se refiere al i-ésimo registro. Esto es simplemente un recuento del número de personas con una frecuencia de muestreo de su clave inferior a k. El recuento es mayor para los k más grandes, ya que si un registro satisface k-anonimato, también satisface (k+1)- anonimato. La medida del riesgo k-anonimato no considera los pesos de la muestra, pero es importante considerar los pesos de la muestra al determinar el nivel requerido de k-anonimato. Si los pesos de la muestra son grandes, un individuo en el conjunto de datos representa a más individuos en la población objetivo, la probabilidad de una coincidencia correcta es menor y, por lo tanto, el umbral requerido puede ser más bajo. Los pesos de muestra grandes van de la mano con conjuntos de datos más pequeños. En un conjunto de datos más pequeño, la probabilidad de encontrar otro registro con la misma clave es menor que en un conjunto de datos más grande. Esta probabilidad está relacionada con el número de registros en la población con una clave particular a través de los pesos muestrales.

En sdcMicro podemos mostrar el número de observaciones que violan un determinado umbral de k-anonimato. En el Bloque 7.4, usamos sdcMicro para calcular la cantidad de infractores para los umbrales \(k=2\) y \(k=3\). Se da tanto el número absoluto de infractores como el número relativo como porcentaje del número de individuos en la muestra. En el ejemplo, cuatro observaciones violan el 2-anonimato y las 10 observaciones violan el 3-anonimato.

Bloque 7.4 Uso de la función print() para mostrar observaciones que violan k-anonimato

print(sdcInitial, 'kAnon')

Para otros niveles de k-anonimato, es posible calcular el número de personas infractoras utilizando los recuentos de frecuencia de muestreo en el objeto sdcMicro. El número de infractores es el número de personas con recuentos de frecuencia de muestreo inferiores al umbral especificado k. En el Bloque 7.5, mostramos un ejemplo de cómo calcular cualquier umbral para k usando las medidas de riesgo ya almacenadas disponibles después de configurar un objeto sdcMicro en R. k se puede reemplazar con cualquier umbral requerido. La elección del umbral requerido que deben cumplir todas las personas en el archivo de microdatos depende de muchos factores y se analiza más adelante en la sección Supresión local sobre la supresión local. En muchas instituciones, los umbrales típicamente requeridos para k-anonimato son 3 y 5.

Bloque 7.5 Violaciones de k-anonimato para distintos valores de k

k=10
sum(sdcInitial@risk$individual[,2] < k)

Es importante tener en cuenta que los valores faltantes (NAs en R 18 ) se tratan como si fueran cualquier otro valor. Dos personas con claves {‘Masculino’, NA, ‘Ocupado’} y {‘Masculino’, ‘Secundaria completa’, ‘Ocupado’} comparten la misma clave y, de manera similar, {‘Masculino’, NA, ‘Ocupado’} y {‘Masculino’, ‘Secundaria incompleta’, ‘Ocupado’} también comparten la misma clave. Por lo tanto, el valor que falta en la primera clave se interpreta primero como ‘Secundaria completa’ y luego como ‘Secundaria incompleta’. Esto se ilustra en la Tabla 7.2.

Tabla 7.2: Conjunto de datos de ejemplo para ilustrar el efecto de los valores faltantes en el k-anonimato
Id Género Nivel educacional Situación laboral \(f_{k}\)
1 Masculino Secundaria completa Ocupado 2
2 Masculino Secundaria incompleta Ocupado 2
3 Masculino NA Ocupado 3

Fuente: Adaptación de (Benschop, Machingauta, and Welch 2021, 32)

Si un conjunto de datos satisface k-anonimato, un intruso siempre encontrará al menos k individuos con la misma combinación de identificadores indirectos. El k-anonimato suele ser un requisito necesario para la anonimización de un conjunto de datos antes de su publicación, pero no es necesariamente un requisito suficiente. La medida de k-anonimato solo se basa en recuentos de frecuencia y no tiene en cuenta (las diferencias en) los pesos de las muestras. Con frecuencia el k-anonimato se logra aplicando primero la recodificación y luego la supresión local y, en algunos casos, mediante la microagregación, antes de utilizar otras medidas de riesgo y métodos de divulgación para reducir aún más el riesgo de divulgación. Estos métodos se analizan en la sección Métodos SDC.

7.5.3 l-diversity

El k-anonimato ha sido criticado por no ser lo suficientemente restrictivo. La información confidencial puede divulgarse incluso si los datos satisfacen el k-anonimato. Esto puede ocurrir en los casos en que los datos contienen variables categóricas confidenciales (de no identificación) que tienen el mismo valor para todas las personas que comparten la misma clave. Ejemplos de tales variables sensibles son aquellas que contienen información sobre el estado de salud de un individuo. La Tabla 7.3 ilustra este problema utilizando los mismos datos que se utilizaron anteriormente, pero agregando una variable sensible, “salud”. Los dos primeros individuos cumplen 2-anonimato para los identificadores indirectos “área”, “género”, “nivel educacional” y “situación laboral”. Esto significa que un intruso encontrará al menos dos personas al hacer coincidir el conjunto de microdatos publicado en función de esos cuatro identificadores indirectos. Sin embargo, si el intruso sabe que alguien pertenece a la muestra y tiene la clave {‘Urbano’, ‘Femenino’, ‘Secundaria incompleta’ y ‘Ocupado’}, con certeza se revela el estado de salud (‘sí’), porque para ambos las observaciones con esta clave tienen el mismo valor. Esta información se revela así sin la necesidad de coincidir exactamente con el individuo. Este no es el caso de los individuos con clave {‘Urbano’, ‘Masculino’, ‘Secundaria completa’, ‘Ocupado’}.

El concepto de l-diversity (distinto) aborda esta deficiencia del k-anonimato. Un conjunto de datos satisface l-diversity si para cada clave k hay por lo menos l diferentes valores para cada una de las variables sensibles. En el ejemplo, los primeros dos individuos satisfacen solo 1-diversity, los individuos 4 y 6 satisfacen 2-diversity. El nivel requerido de l-diversity depende del número de valores posibles que puede tomar la variable sensible. Si la variable sensible es una variable binaria, el nivel más alto de l-diversity que se puede conseguir es 2. Una muestra única siempre solo satisfará 1-diversity.

Para computar l-diversity para variables sensibles en sdcMicro, se puede usar la función ldiversity(). Esto se ilustra en el Bloque 7.6. Como argumentos, especificamos los nombres de las variables sensibles 19 en el archivo, así como una constante para l-diversity 20 y el código de valores faltantes en los datos. La salida se guarda en el slot de “riesgo” del objeto sdcMicro. El resultado muestra el mínimo, máximo, media y cuantiles de las l-puntuaciones de diversidad para todos los individuos de la muestra. El resultado del Bloque 7.6 reproduce los resultados según los datos de la Tabla 7.3.

Tabla 7.3: Ilustración de l-diversity
Id Área Género Nivel educacional Situación laboral Salud \(f_{k}\) \(F_{k}\) l-diversity
1 Urbano Femenino Secundaria incompleta Ocupado Enfermo 2 360 1
2 Urbano Femenino Secundaria incompleta Ocupado Enfermo 2 360 1
3 Urbano Femenino Primaria incompleta No FL Enfermo 1 215 1
4 Urbano Masculino Secundaria completa Ocupado Enfermo 2 152 2
5 Rural Femenino Secundaria completa Desocupado Enfermo 1 186 1
6 Urbano Masculino Secundaria completa Ocupado Sano 2 152 2
7 Urbano Femenino Primaria completa No FL Sano 1 180 1
8 Urbano Masculino Post secundaria Desocupado Enfermo 1 215 1
9 Urbano Femenino Secundaria incompleta No FL Sano 2 262 2
10 Urbano Femenino Secundaria incompleta No FL Enfermo 2 262 2

Fuente: Adaptación de (Benschop, Machingauta, and Welch 2021, 33)

Bloque 7.6 Función para l-diversity en sdcMicro

 # Calculando l-diversity

 sdcInitial <- ldiversity(obj = sdcInitial, ldiv_index = c("Salud"), 
                          l_recurs_c = 2, missing = NA)
 # Resultado para l-diversity
 sdcInitial@risk$ldiversity
 
 # l-diversity score para cada registro
 sdcInitial@risk$ldiversity[,'Salud_Distinct_Ldiversity']

l-diversity es útil si los datos contienen variables sensibles categóricas que no son identificadores indirectos en sí mismos. No es posible seleccionar identificadores indirectos para calcular la l-diversity. La l-diversity debe calcularse para cada variable sensible por separado.

7.6 Medidas de riesgo para variables continuas

El principio de rareza o unicidad de combinaciones de identificadores indirectos (claves) no es útil para variables continuas, porque es probable que todos o muchos individuos tengan claves únicas. Por lo tanto, se explotan otros enfoques para medir el riesgo de divulgación de las variables continuas. Estos métodos se basan en la unicidad de los valores en la vecindad de los valores originales. La unicidad se define de diferentes formas: en términos absolutos (medida de intervalo) o en términos relativos (vinculación de registros). La mayoría de las medidas son medidas a posteriori: se evalúan después de anonimizar los datos sin procesar, comparar los datos tratados con los datos sin procesar y evaluar para cada individuo la distancia entre los valores en los datos sin procesar y los tratados. Esto significa que estos métodos no son útiles para identificar personas en riesgo dentro de los datos sin procesar, sino que muestra la distancia/diferencia entre el conjunto de datos antes y después de la anonimización y, por lo tanto, puede interpretarse como una evaluación del método de anonimización. Por esa razón, se asemejan a las medidas de pérdida de información discutidas en la sección Medición de la utilidad y la pérdida de información. Finalmente, las medidas de riesgo para identificadores indirectos continuos también se basan en la detección de valores atípicos. Los valores atípicos juegan un papel importante en la reidentificación de estos registros.

7.6.1 Vinculación de registros (o coincidencia de registros)

Vinculación de registros (o Record linkage, en inglés) es un método a posteriori que evalúa el número de vínculos correctos al vincular los valores perturbados con los valores originales. El algoritmo de vinculación se basa en la distancia entre el original y los valores perturbados (es decir, vinculación de registros basada en la distancia). Los valores perturbados se emparejan con el individuo más cercano. Es importante señalar que este método no brinda información sobre el riesgo inicial, sino que es una medida para evaluar el algoritmo de perturbación (es decir, está diseñado para indicar el nivel de incertidumbre introducido en la variable al contar la cantidad de registros que podría coincidir correctamente).

Los algoritmos de vinculación de registros difieren con respecto a qué medida de distancia se utiliza. Cuando una variable tiene una escala muy diferente a la de otras variables continuas en el conjunto de datos, se recomienda volver a escalar las variables antes de usar la vinculación de registros. Escalas muy diferentes pueden dar lugar a resultados no deseados al medir la distancia multivariada entre registros en función de varias variables continuas. Dado que estos métodos se basan tanto en datos sin procesar como en datos tratados, los ejemplos de sus aplicaciones requieren la introducción de métodos SDC y, por lo tanto, se posponen a los estudios de casos en la sección Caso de estudio.

Además de la vinculación de registros basada en la distancia, otro método de vinculación es la vinculación de registros probabilísticos. La literatura muestra, sin embargo, que los resultados de la vinculación de registros basados en la distancia son mejores que los resultados de la vinculación de registros probabilísticos. Las personas en los datos tratados que están vinculadas a las personas correctas en los datos sin procesar se consideran en riesgo de divulgación.

7.6.2 Medida de intervalo

La aplicación exitosa de un método SDC debería dar como resultado valores perturbados que no se consideran demasiado cercanos a sus valores iniciales; si el valor es relativamente cercano, la reidentificación puede ser relativamente fácil. En la aplicación de medidas de intervalo, se crean intervalos alrededor de cada valor perturbado y luego se determina si el valor original de esa observación perturbada está contenido en este intervalo. Los valores que están dentro del intervalo alrededor del valor inicial después de la perturbación se consideran demasiado cercanos al valor inicial y, por lo tanto, no son seguros y necesitan más perturbaciones. Los valores que están fuera de los intervalos se consideran seguros. El tamaño de los intervalos se basa en la desviación estándar de las observaciones y un parámetro de escala. Este método está implementado en la función dRisk() en sdcMicro. El Bloque 7.7 muestra cómo imprimir o mostrar el valor de riesgo calculado por sdcMicro comparando las variables de ingresos antes y después de la anonimización. “sdcObj” es un objeto sdcMicro y “compExp“ es un vector que contiene los nombres de las variables de ingresos. El tamaño de los intervalos es k veces la desviación estándar, donde k es un parámetro en la función dRisk(). El más largo k, cuanto más grandes son los intervalos y, por lo tanto, mayor es el número de observaciones dentro del intervalo construidas alrededor de sus valores originales y mayor es la medida de riesgo. El resultado 1 indica que todas (100 por ciento) las observaciones están fuera del intervalo de 0,1 veces la desviación estándar alrededor de los valores originales.

Bloque 7.7 Ilustración de medida de intervalo

 dRisk(obj = sdcObj@origData[,compExp], xm = sdcObj@manipNumVars[,compExp],
       k = 0.1)
 [1] 1

Para la mayoría de los valores, este es un enfoque satisfactorio. Sin embargo, no es una medida suficiente para valores atípicos. Después de la perturbación, los valores atípicos seguirán siendo valores atípicos y se pueden volver a identificar fácilmente, incluso si están lo suficientemente lejos de sus valores iniciales. Por lo tanto, los valores atípicos deben tratarse con precaución.

7.6.3 Detección de valores atípicos

Los valores atípicos son importantes para medir el riesgo de reidentificación en microdatos continuos. Los datos continuos suelen estar sesgados, especialmente a la derecha. Esto significa que hay algunos valores atípicos con valores muy altos en relación con las otras observaciones de la misma variable. Algunos ejemplos son los ingresos en los datos de los hogares, donde solo unas pocas personas/hogares pueden tener ingresos muy altos, o los datos de facturación de empresas que son mucho más grandes que otras empresas de la muestra. En casos como estos, incluso si estos valores se perturban, aún puede ser fácil identificar estos valores atípicos, ya que seguirán siendo los valores más grandes incluso después de la perturbación (la perturbación habrá creado incertidumbre en cuanto al valor exacto, pero debido a que el valor comenzó mucho más lejos de otras observaciones, aún puede ser fácil vincularlo con el individuo de altos ingresos o la empresa muy grande). Los ejemplos serían el único médico en un área geográfica con altos ingresos o una sola gran empresa en un tipo de industria. Por lo tanto, la identificación de valores atípicos en datos continuos es un paso importante cuando se identifican personas con alto riesgo. En la práctica, identificar los valores de una variable continua que son mayores que un valor predeterminado p%-percentil podría ayudar a identificar valores atípicos y, por lo tanto, unidades con mayor riesgo de identificación. El valor de p depende de la asimetría de los datos.

Podemos calcular el p%-percentil de una variable continua en R y mostrar los individuos que tienen ingresos superiores a este percentil. El Bloque 7.8 proporciona una ilustración del percentil 90.

Bloque 7.8 Cómputo del percentil 90 % de la variable INCWAGE

setwd("../Capacitación/GitHub") # directorio de trabajo

fname = "data.dta" # nombre del archivo
library(haven) # carga el paquete requerido para la función de lectura/escritura
               # para archivos STATA
file <- read_dta(fname) 

# Cómputo de 90 % percentil para variable INCWAGE
 perc90 <- quantile(file[,'INCWAGE'], 0.90, na.rm = TRUE)

 # Muestra ID de observaciones con valores para INCWAGE mayores al 90 % percentil
 file[(file[, 'INCWAGE'] >= perc90), 'IDP']

Un segundo enfoque para la detección de valores atípicos es una medida a posteriori que compara los datos tratados y sin procesar. Se construye un intervalo alrededor de los valores perturbados como se describe en la sección anterior. Si los valores originales caen dentro del intervalo alrededor de los valores perturbados, los valores perturbados se consideran inseguros ya que están demasiado cerca de los valores originales. Existen diferentes formas de construir dichos intervalos, como intervalos basados en rangos e intervalos basados en desviación estándar. Templ and Meindl (2008) proponen una alternativa robusta para estos intervalos. Construyen los intervalos en función de la distancia robusta de Mahalanobis (RMD, por su sigla en inglés) al cuadrado de los valores individuales. El RMD escala los intervalos de manera que los valores atípicos obtienen intervalos más grandes y, por lo tanto, deben tener una perturbación mayor para que se consideren seguros que los valores que no son atípicos. Este método se implementa en sdcMicro en la función dRiskRMD(), que es una extensión de la función dRisk().

7.7 Riesgo global

Para construir una medida de riesgo agregado a nivel global para el conjunto de datos completo, podemos agregar las medidas de riesgo a nivel individual de varias maneras. Las medidas de riesgo global deben usarse con precaución: detrás de un riesgo global aceptable pueden esconderse algunos registros de muy alto riesgo que se compensan con muchos registros de bajo riesgo.

7.7.1 Media de las medidas de riesgo individuales

Una forma sencilla de agregar las medidas de riesgo individuales es tomar la media de todos los individuos de la muestra, que es igual a sumar todas las claves de la muestra si se multiplica por las frecuencias de muestra de estas claves y se divide por el tamaño de la muestra, \(n\):

\[R_{1}=\frac{1}{n}\sum_{i} r_{k}=\frac{1}{n}\sum_{k}f_{k}r_{k},\]

donde \(r_{k}\) es el riesgo individual de clave \(k\) que el i-ésimo registro comparte (ver la sección Identificadores indirectos categóricos y recuentos de frecuencia). Esta medida se informa como riesgo global en sdcMicro, se almacena en el slot de “riesgo” y se puede imprimir como se muestra en el Bloque 7.9. Indica que la probabilidad de reidentificación promedio es 0,01582 o 0,1582%.

Bloque 7.9 Cómputo de la medida de riesgo global

# Riesgo global (probabilidad promedio de re-identificación)
 sdcInitial@risk$global$risk

El riesgo global en los datos de ejemplo de la Tabla 7.1 es 0,01582, que es la proporción esperada de todos los individuos de la muestra que un intruso podría volver a identificar. Otra forma de expresar el riesgo global es el número de reidentificaciones esperadas, \(n*R_{1}\), que es en el ejemplo 10 * 0,01582. El número esperado de reidentificaciones también se guarda en el objeto sdcMicro. El Bloque 7.10 muestra cómo imprimir esto.

Bloque 7.10 Cómputo del número esperado de reidentificaciones

#  # Riesgo global(Número esperado de re-identificaciones)
 sdcInitial@risk$global$risk_ER

7.7.2 Recuento de personas con riesgos superiores a un cierto umbral

Todos los individuos pertenecientes a la misma clave tienen el mismo riesgo individual, \(r_{k}\). Otra forma de expresar el riesgo total en la muestra es el número total de observaciones que superan un determinado umbral de riesgo individual. La fijación del umbral puede ser absoluta (por ejemplo, todas aquellas personas que tengan un riesgo de divulgación superior a 0,05 o 5%) o relativa (por ejemplo, todas aquellas personas con riesgos superiores al cuartil superior del riesgo individual). El Bloque 7.11 muestra cómo utilizando R, se contaría el número de observaciones con un riesgo de reidentificación individual superior al 5%. En el ejemplo, ninguna persona tiene un riesgo de divulgación superior a 0,05.

Bloque 7.11 Número de personas con riesgo individual superior al umbral 0,05

 sum(sdcInitial@risk$individual[,1] > 0.05)

Estos cálculos se pueden usar para tratar los datos de las personas cuyos valores de riesgo están por encima de un umbral predeterminado. Más adelante veremos que hay métodos en sdcMicro, como localSupp(), que se pueden usar para suprimir valores de ciertas variables clave para aquellas personas con riesgo por encima de un umbral específico. Esto se explica con más detalle en la sección Supresión local.

7.8 Riesgo jerárquico (o del hogar)

En muchas encuestas sociales, los datos tienen una estructura jerárquica donde un individuo pertenece a una entidad de nivel superior (ver la sección Niveles de riesgo). Ejemplos típicos son los hogares en las encuestas sociales o los alumnos en las escuelas. La reidentificación de un miembro del hogar también puede conducir a la reidentificación de los otros miembros del hogar. Por tanto, es fácil ver que, si tenemos en cuenta la estructura del hogar, el riesgo de reidentificación es el riesgo de que al menos uno de los miembros del hogar sea reidentificado.

\[r^h=P(A_{1}\bigcup A_{2}\bigcup \dots \bigcup A_{J})=1-\prod_{j=1}^J 1-P(A_{j}), \] donde \(A_{j}\) es el evento que el j-ésimo miembro del hogar sea identificado y \(P(A_{j})=r_{k}\) es el riesgo de divulgación individual del j-ésimo miembro. Por ejemplo, si un hogar tiene tres miembros con riesgos de divulgación individuales en función de sus respectivas claves 0,02, 0,03 y 0,03, respectivamente, el riesgo del hogar es

\[1-((1-0,02)(1-0,03)(1-0,03))=0,078\]

El riesgo jerárquico o del hogar no puede ser menor que el riesgo individual, y el riesgo del hogar es siempre el mismo para todos los miembros del hogar. El riesgo del hogar debe utilizarse en los casos en que los datos contengan una estructura jerárquica, es decir, cuando la estructura del hogar esté presente en los datos. Usando sdcMicro, si se especifica un identificador de hogar (en el argumento hhId en la función createSdcObj()) al crear un objeto sdcMicro, el riesgo del hogar se calculará automáticamente. El Bloque 7.12 muestra cómo imprimir estas medidas de riesgo.

Bloque 7.12 Cómputo del riesgo del hogar y número esperado de reidentificaciones

# Riesgo del hogar
 sdcInitial@risk$global$hier_risk

 # Riesgo del hogar (Número esperado de reidentificaciones)
 sdcInitial@risk$global$hier_risk_ER

El tamaño de un hogar es un identificador importante en sí mismo, especialmente para hogares grandes. Sin embargo, la supresión de la variable del tamaño real (por ejemplo, el número de miembros del hogar) no es suficiente para eliminar esta información del conjunto de datos, ya que un simple recuento de los miembros del hogar para un hogar en particular permitirá reconstruir esta variable siempre que un ID del hogar esté en los datos, lo que permite asignar individuos a los hogares. Señalamos esto para la atención del lector ya que es importante.

7.9 Referencias

Referencias

———. 2021. “Statistical Disclosure Control: A Practice Guide.” World Bank, 195. https://sdcpractice.readthedocs.io/en/latest/.
Elliot, Mark, Susan Lomax, Elaine Mackey, and Kingsley Purdam. 2010. “Data Environment Analysis and the Key Variable Mapping System.” In, edited by Josep Domingo-Ferrer and Emmanouil Magkos, 138–47. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-642-15838-4_13.
Hundepool, Anco, Josep Domingo-Ferrer, Luisa Franconi, Sarah Giessing, Eric Schulte Nordholt, Keith Spicer, and Peter Paul De Wolf. 2012. Statistical Disclosure Control. John Wiley & Sons, Ltd. https://doi.org/10.1002/9781118348239.indauth.
Lambert, Diane. 1993. “Measures of Disclosure Risks and Harm.” Journal of Official Statistics 9 (2): 1–36. https://www.scb.se/contentassets/ca21efb41fee47d293bbee5bf7be7fb3/measures-of-disclosure-risk-and-harm.pdf.
Templ, Matthias, and Bernhard Meindl. 2008. “Robust Statistics Meets SDC: New Disclosure Risk Measures for Continuous Microdata Masking.” In, edited by Josep Domingo-Ferrer and Yücel Saygın, 177–89. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-540-87471-3_15.

  1. Recodificar una variable continua a veces es útil en los casos en que los datos contienen solo unas pocas variables continuas. Veremos en la sección Riesgo individual que muchos métodos utilizados para el cálculo del riesgo dependen de si las variables son categóricas. También veremos que es más fácil para la medición del riesgo si los datos contienen solo variables categóricas o solo continuas.↩︎

  2. Esto se discute con mayor detalle en las siguientes secciones. En los casos en que el número de valores posibles sea grande, se recomienda recodificar la variable, o partes del conjunto en el que toma valores, para obtener menos valores distintos.↩︎

  3. No todos los datos externos son necesariamente de dominio público. También se deben tener en cuenta los conjuntos de datos de propiedad privada o los conjuntos de datos que no se divulgan para determinar el escenario de divulgación adecuado.↩︎

  4. Consulte la sección Objetos de la clase sdcMicroObj para obtener más información sobre los slots y la estructura del objeto sdcMicro.↩︎

  5. Los supuestos para esta medida de riesgo son estrictos y el riesgo se estima en muchos casos mayor que el riesgo real. Entre otras suposiciones, se supone que todos los individuos de la muestra también están incluidos en el archivo externo utilizado por el intruso para compararlos. Si no es así, el riesgo es mucho menor; si el individuo en el archivo liberado no está incluido en el archivo externo, la probabilidad de una coincidencia correcta es cero. Otras suposiciones son que los archivos no contienen errores y que ambos conjuntos de datos se recopilaron simultáneamente, es decir, contienen la misma información. Estos supuestos a menudo no se cumplen en general, pero son necesarios para el cálculo de una medida. Un ejemplo de una violación de las últimas suposiciones podría ocurrir si los conjuntos de datos se recopilan en diferentes puntos en el tiempo y los registros han cambiado. Esto podría suceder cuando las personas se mudan o cambian de trabajo y hace imposible la coincidencia correcta. Los supuestos son conservadores y asumen el mayor riesgo de divulgación.↩︎

  6. Consulte la sección Objetos de la clase sdcMicroObj para obtener más información sobre los slots y la estructura del objeto sdcMicro.↩︎

  7. En sdcMicro, es importante utilizar el código de valor faltante estándar NA en lugar de otros códigos, como 9999 o cadenas. En la sección Valores faltantes, se analizó más detalladamente cómo establecer otros códigos de valores faltantes de NA en R. Esto es necesario para garantizar que los métodos de sdcMicro funcionen correctamente. Cuando los valores faltantes tienen códigos distintos de NA, los códigos de valores faltantes se interpretan como un nivel de factor distinto en el caso de las variables categóricas.↩︎

  8. Alternativamente, las variables sensibles se pueden especificar al crear el objeto sdcMicro usando la función createSdcObj() en el argumento sensibleVar. Esto se explica con más detalle en la sección Objetos de la clase sdcMicroObj. En ese caso, no es necesario especificar el argumento ldiv_index en la función ldiversity(), y las variables en el argumento sensibleVar se usarán automáticamente para calcular l-diversity.↩︎

  9. Además de l-diversity distintos, hay otros métodos de l-diversity: entropía y recursivo. l-diversity distinto es el más utilizado.↩︎