Capítulo 8 Métodos SDC

Esta sección describe los métodos SDC más utilizados. Todos los métodos se pueden implementar en R utilizando el paquete sdcMicro. Discutimos qué método es más adecuado para cada tipo de datos, tanto en términos de características como del tipo de dato. Además, se discuten opciones como los parámetros específicos de cada método, así como sus impactos. Las conclusiones pretenden ser orientativas, pero deben utilizarse con precaución, ya que cada operación estadística genera datos con características diferentes y las recomendaciones del documento no siempre serán las más adecuadas para sus datos en particular.

Para determinar qué métodos de anonimización son adecuados para variables y/o conjuntos de datos específicos, comenzamos presentando algunas clasificaciones de los métodos SDC.

8.1 Clasificación de los métodos SDC

Los métodos SDC pueden clasificarse en no perturbativos y perturbativos (A. Hundepool et al. 2012).

• Los métodos no perturbativos reducen el detalle de los datos mediante la generalización o la supresión de ciertos valores (enmascaramiento) sin distorsionar la estructura de los datos.
• Los métodos perturbativos no suprimen los valores del conjunto de datos, sino que alteran los valores para limitar el riesgo de divulgación creando incertidumbre en torno a los valores reales. Tanto los métodos no perturbativos como los perturbativos pueden utilizarse para variables categóricas y continuas.

También distinguimos entre métodos probabilísticos y deterministas SDC.

Los métodos probabilísticos dependen de un mecanismo de probabilidad o de un mecanismo de generación de números aleatorios. Cada vez que se utiliza un método probabilístico, se genera un resultado diferente. Para estos métodos se suele recomendar que se establezca una semilla (con la función set.seed()) para el generador de números aleatorios si se quiere producir resultados replicables.

Los métodos deterministas siguen un algoritmo determinado y producen los mismos resultados si se aplican repetidamente a los mismos datos con el mismo conjunto de parámetros.

Los métodos SDC para microdatos pretenden evitar la revelación de identidad y de atributos. Para cada tipo de control de la divulgación se utilizan diferentes métodos SDC. Métodos como la recodificación y la supresión local se aplican a los identificadores indirectos para evitar la divulgación de identidad, mientras que la codificación superior de un identificador indirecto (por ejemplo, los ingresos) o la perturbación de una variable sensible evitan la divulgación de atributos.

Discutiremos los métodos SDC que se implementan en el paquete sdcMicro o que pueden implementarse fácilmente en R. Estos son los métodos más comúnmente aplicados en la literatura y utilizados en la mayoría de las agencias con experiencia en el uso de estos métodos. La Tabla 8.1 ofrece una visión general de los métodos de SDC discutidos en esta guía, su clasificación, los tipos de datos a los que son aplicables y los nombres de sus funciones en el paquete sdcMicro.

Tabla 8.1: Métodos SDC y funciones correspondientes en sdcMicro

Método	Clasificación del método SDC	Tipo de datos	Función en sdcMicro
Recodificación Global	no perturbativo, determinista	continuo y categórico	globalRecode , groupVars
Codificación Superior e Inferior	no perturbativo, determinista	continuo y categórico	topBotCoding
Supresión Local	no perturbativo, determinista	categórico	localSuppression,localSupp
PRAM	perturbativo, probabilístico	categórico	pram
Micro agregación	perturbativo, probabilístico	continuo	microaggregation
Adición de Ruido	perturbativo, probabilístico	continuo	addNoise
Shuffling	perturbativo, probabilístico	continuo	shuffle
Rank swapping	perturbativo, probabilístico	continuo	rankSwap

8.2 Métodos no perturbativos

8.2.1 Recodificación

La recodificación es un método determinista utilizado para disminuir el número de categorías o valores distintos de una variable. Se realiza combinando o agrupando categorías para las variables categóricas o construyendo intervalos para las variables continuas. La recodificación se aplica a todas las observaciones de una determinada variable y no solo a las que corren el riesgo de ser reveladas. Existen dos tipos generales de recodificación: la recodificación global y la codificación superior e inferior.

8.2.1.1 Recodificación global

La recodificación global combina varias categorías de una variable categórica o construye intervalos para variables continuas. Esto reduce el número de categorías disponibles en los datos y, potencialmente, el riesgo de divulgación, especialmente para las categorías con pocas observaciones, pero también, y esto es importante, reduce el nivel de detalle de la información disponible para el analista. Para ilustrar la recodificación, utilizamos el siguiente ejemplo. Supongamos que tenemos cinco regiones en nuestro conjunto de datos. Algunas regiones son muy pequeñas y, cuando se combinan con otras variables clave del conjunto de datos, producen un alto riesgo de reidentificación para algunos individuos de esas regiones. Una forma de reducir el riesgo sería combinar algunas de las regiones al recodificarlas. Podríamos, por ejemplo, hacer tres grupos de los cinco, llamarlos “Norte”, “Centro” y “Sur” y en consecuencia reetiquetar los valores. De este modo, el número de categorías de la región variable se reduce de cinco a tres.

Nota: Cualquier agrupación debe ser una agrupación pertinente para los objetivos analíticos de la operación estadística y no una unión aleatoria de categorías.

Algunos ejemplos serían agrupar las comunas en provincias, las regiones en macrozonas o las categorías detalladas de agua limpia. Agrupar todas las regiones pequeñas sin proximidad geográfica no es necesariamente la mejor opción desde el punto de vista de los servicios públicos. La Tabla 8.2 lo ilustra con un conjunto de datos de ejemplo muy simplificado. Antes de la recodificación, tres individuos tienen claves distintas, mientras que después de la recodificación (agrupando la “Región 1” y la “Región 2” en el “Norte”, la “Región 3” en el “Centro” y la “Región 4” y la “Región 5” en el “Sur”), el número de claves distintas se reduce a cuatro y la frecuencia de cada clave es de al menos dos, basándose en los tres identificadores indirectos seleccionados. Los recuentos de la frecuencia de las claves \(fk\) se muestran en la última columna de la Tabla 8.2. Un intruso encontraría al menos dos individuos para cada clave y no podría distinguir más entre los individuos 1 - 3, los individuos 4 y 6, los individuos 5 y 7 y los individuos 8 - 10, basándose en las variables clave seleccionadas.

Tabla 8.2: Ilustración del efecto de la recodificación en los recuentos de frecuencia de las variables clave

Antes de recodificar					Después de recodificar
Individuo	Región	Sexo	Religión	\(f_k\)	Región	Sexo	Religión	\(f_k\)
1	Región 1	Mujer	Católica	1	Norte	Mujer	Católica	3
2	Región 2	Mujer	Católica	2	Norte	Mujer	Católica	3
3	Región 2	Mujer	Católica	2	Norte	Mujer	Católica	3
4	Región 3	Mujer	Protestante	2	Centro	Mujer	Protestante	2
5	Región 3	Hombre	Protestante	1	Centro	Hombre	Protestante	2
6	Región 3	Mujer	Protestante	2	Centro	Mujer	Protestante	2
7	Región 3	Hombre	Protestante	2	Centro	Hombre	Protestante	2
8	Región 4	Hombre	Musulmán	2	Sur	Hombre	Musulmán	3
9	Región 4	Hombre	Musulmán	2	Sur	Hombre	Musulmán	3
10	Región 5	Hombre	Musulmán	1	Sur	Hombre	Musulmán	3

La recodificación suele ser el primer paso de un proceso de anonimización. Puede utilizarse para reducir el número de combinaciones únicas de valores de las variables clave. Por lo general, esto aumenta los recuentos de frecuencia de la mayoría de las claves y reduce el riesgo de divulgación. La reducción del número de combinaciones posibles se ilustra en la Tabla 8.3 con los identificadores indirectos “región”, “estado civil” y “edad”. La Tabla 8.3 muestra el número de categorías de cada variable y el número de combinaciones teóricamente posibles, que es el producto del número de categorías de cada identificador indirecto, antes y después de la recodificación. La “edad” se interpreta como una variable semicontinua y se trata como una variable categórica. El número de combinaciones posibles y, por tanto, el riesgo de reidentificación se reducen en gran medida con la recodificación. Hay que tener en cuenta que el número de combinaciones posibles es un número teórico; en la práctica, pueden incluirse combinaciones muy improbables, como edad = 3 y estado civil = viudo, y el número real de combinaciones en un conjunto de datos puede ser inferior.

Tabla 8.3: Ilustración del efecto de la recodificación en el número de combinaciones teóricamente posibles de un conjunto de datos

Número de categorías	Región	Estado civil	Edad	Posibles combinaciones
antes de la recodificación	20	8	100	16.000
después de la recodificación	6	6	15	540

Los principales parámetros para la recodificación global son el tamaño de los nuevos grupos, así como la definición de los valores que se agrupan en las nuevas categorías.

Nota: Hay que tener cuidado de elegir las nuevas categorías, deberían generarse en función del uso de los datos por parte de los usuarios finales y de minimizar la pérdida de información como resultado de la recodificación.

Podemos observarlo mediante tres ejemplos:

• Variable de edad: Las categorías de edad deben elegirse de forma que sigan permitiendo a los usuarios de los datos realizar cálculos relevantes para el tema que se está estudiando. Por ejemplo, si es necesario calcular indicadores para niños de edades comprendidas entre los 6 y los 11 años y entre los 12 y los 17 años, además, es necesario agrupar la edad para reducir el riesgo, hay que tener cuidado de crear intervalos de edad que sigan permitiendo realizar los cálculos. Una agrupación satisfactoria podría ser, por ejemplo, 0 - 5, 6 - 11, 12 - 17, etc., mientras que una agrupación 0 - 10, 11 - 15, 16 - 18 destruiría la utilidad de los datos para estos usuarios. Aunque es una práctica habitual crear intervalos (grupos) de igual anchura (tamaño), también es posible (si los usuarios de los datos lo requieren) recodificar solo una parte de las variables y dejar algunos valores como estaban originalmente. Esto podría hacerse, por ejemplo, recodificando todas las edades superiores a 20 años, pero dejando las inferiores a 20 años tal y como están. Si los métodos SDC distintos de la recodificación se van a utilizar más tarde o en un paso siguiente, hay que tener cuidado al aplicar la recodificación solo a una parte de la distribución, ya que esto podría aumentar la pérdida de información debida a los otros métodos, ya que la agrupación no protege las variables no agrupadas. La recodificación parcial seguida de métodos de supresión como la supresión local puede, por ejemplo, conducir a un número de supresiones mayor del deseado o necesario en caso de que la recodificación se realice para todo el rango de valores (ver la siguiente sección de Supresión local). En el ejemplo anterior, el número de supresiones de los valores inferiores a 20 será probablemente mayor que para los valores del rango recodificado. El número desproporcionadamente alto de supresiones en este rango de valores que no se recodifican puede conducir a una mayor pérdida de utilidad para estos grupos.

• Variables geográficas: Si los datos originales especifican información de nivel administrativo en detalle, por ejemplo, hasta el nivel de comuna, entonces potencialmente esos niveles inferiores podrían ser recodificados o agregados en niveles administrativos superiores, por ejemplo, la provincia, para reducir el riesgo. Al hacerlo, hay que tener en cuenta lo siguiente: La agrupación de comunas en niveles abstractos que se cruzan con diferentes provincias haría que el análisis de datos a nivel comunal o provincial fuera un reto. Se debe tener cuidado de entender lo que el usuario requiere y la intención del estudio. Si un componente clave de la encuesta es realizar un análisis a nivel comunal, la agregación a nivel provincial podría perjudicar la utilidad de los datos para el usuario. La recodificación debería aplicarse si el nivel de detalle de los datos no es necesario para la mayoría de los usuarios de los datos y para evitar un gran número de supresiones cuando se utilicen posteriormente otros métodos SDC. Si los usuarios necesitan información a un nivel más detallado, otros métodos, como los Métodos perturbativos, podrían ofrecer una solución mejor que la recodificación.

• Instalaciones sanitarias: Un ejemplo de una situación en la que un alto nivel de detalle podría no ser necesario y la recodificación podría hacer muy poco daño a la utilidad es el caso de una variable detallada de instalaciones sanitarias en el hogar que enumera las respuestas para 20 tipos de inodoros. Es posible que los investigadores solo necesiten distinguir entre instalaciones de inodoros mejoradas y no mejoradas y que no necesiten la clasificación exacta de hasta 20 tipos. La información detallada de los tipos de inodoros puede utilizarse para volver a identificar a los hogares, mientras que la recodificación en dos categorías -instalaciones mejoradas y no mejoradas- reduce el riesgo de reidentificación y, en este contexto, apenas reduce la utilidad de los datos. Este enfoque puede aplicarse a cualquier variable con muchas categorías en las que los usuarios de los datos no estén interesados en los detalles, sino en algunas categorías agregadas. La recodificación aborda la agregación para los usuarios de los datos y al mismo tiempo protege los microdatos. Es importante hacer un balance de las agregaciones utilizadas por los usuarios.

La recodificación debe aplicarse solo si la eliminación de la información detallada de los datos no perjudica a la mayoría de las personas usuarias. Si los usuarios necesitan información a un nivel más detallado, entonces la recodificación no es apropiada y otros métodos, como los perturbativos, podrían funcionar mejor.

En sdcMicro existen diferentes opciones de recodificación global. En los siguientes párrafos, damos ejemplos de recodificación global con las funciones groupAndRename() y globalRecode(). La función groupAndRename() se utiliza generalmente para las variables categóricas y la función globalRecode() para las variables continuas. Por último, discutimos el uso del redondeo para reducir el detalle en las variables continuas.

8.2.1.1.1 Recodificación de una variable categórica mediante la función sdcMicro groupAndRename()

Supongamos que se ha creado un objeto de la clase sdcMicro, que se llama sdcInitial (véase el apartado Objetos de la clase sdcMicroObj cómo crear objetos de la clase sdcMicro). En el Bloque 8.1, la variable “sizeRes” tiene cuatro categorías diferentes: “capital”, “ciudad grande”, “ciudad pequeña”, “pueblo” y “campo”). Las tres primeras se recodifican o reagrupan como “urbano” y la categoría “campo” pasa a llamarse “rural”. En los argumentos de la función, especificamos las categorías que se van a agrupar (anterior) y los nombres de las categorías después de la recodificación (posterior). Es importante que los vectores “anterior” y “posterior” tengan la misma longitud. Por lo tanto, tenemos que repetir “urbano” tres veces en el vector (posterior) para que coincida con los tres valores diferentes que se recodifican en “urbano”.

Nota: La función groupAndRename() solo funciona en variables tipo factor.

Nos referimos a la sección Clases en R sobre cómo cambiar la clase de una variable.

Cargar librerías.

require(dplyr)
require(foreign)
require(sdcMicro)

Cargaremos la base en formato de dta (stata).

#directorio de trabajo
#getwd()
fname <- "data/data.dta"
file <- read.dta(fname, convert.factors = TRUE)

Ajustaremos las variables a factores.

# Crear variables área y etnia para evaluar recodificación

area_names <- c("capital, large city", "small city", "town", "countryside")
area <- sample(area_names[1:3], nrow(file[file$URBRUR==1,]), replace=TRUE, prob=c(0.60,0.27, 0.13))

file <- file %>% mutate(sizeRes = ifelse(URBRUR==1, area, area_names[4])) %>% relocate(sizeRes, .after = URBRUR) %>%
  mutate(sizeRes = factor(sizeRes, levels = area_names))

etnia_names <- c("mapuche","diaguita","atacameno","otra","No aplica")
etnia <- sample(etnia_names, nrow(file), replace=TRUE, prob=c(0.2,0.1,0.1,0.1, 0.95))


file <- file %>% mutate(etnia = etnia) %>% mutate(etnia = factor(etnia, levels = etnia_names))


selectedKeyVarsHH = c("sizeRes","AGEYRS", "GENDER", "REGION", "etnia","RELIG") #,
#selectedKeyVarsHH = c("URBRUR", "REGION", "HHSIZE", "OWNAGLAND", "RELIG")

file$URBRUR    <- as.factor(file$URBRUR)
file$REGION    <- as.factor(file$REGION)
file$OWNHOUSE  <- as.factor(file$OWNHOUSE)
file$OWNAGLAND <- as.factor(file$OWNAGLAND)
file$RELIG     <- as.factor(file$RELIG)


numVarsHH      <- c("LANDSIZEHA", "TANHHEXP", "TFOODEXP", "TALCHEXP", "TCLTHEXP", "THOUSEXP", 
                    "TFURNEXP", "THLTHEXP", "TTRANSEXP", "TCOMMEXP", "TRECEXP", "TEDUEXP", 
                    "TRESTHOTEXP", "TMISCEXP", "INCTOTGROSSHH", "INCRMT", "INCWAGE", "INCFARMBSN", 
                    "INCNFARMBSN", "INCRENT", "INCFIN", "INCPENSN", "INCOTHER")

pramVarsHH     <- c("ROOF", "TOILET", "WATER", "ELECTCON", "FUELCOOK", "OWNMOTORCYCLE", "CAR", "TV", "LIVESTOCK")
weightVarHH    <- c("WGTPOP")

# Ajuste strata

file$strata_region <- file$REGION
strata_var <- c("strata_region")

# Ajuste para transformar factores
file[,c(pramVarsHH)] <- lapply(file[,c(pramVarsHH)], as.factor)


HHVars <- c("IDH", selectedKeyVarsHH, pramVarsHH, numVarsHH, weightVarHH, strata_var) #agrega strata
fileHH <- file
fileHH <- fileHH[which(!duplicated(fileHH$IDH)),]
sdcHH <- createSdcObj(dat=fileHH, keyVars=selectedKeyVarsHH, pramVars=pramVarsHH, weightVar=weightVarHH, numVars = numVarsHH, strataVar = "strata_region")

sdcInitial <- sdcHH
sdc_respaldo <- sdcHH

Bloque 8.1 Uso de la función sdcMicro groupAndRename() para recodificar una variable categórica

# Frequencias de sizeRes antes de recodificar
table(sdcInitial@manipKeyVars$sizeRes)

## 
## capital, large city          small city                town         countryside 
##                 792                 348                 176                 684

# Recodificar urbano
sdcInitial  <-  groupAndRename(sdcInitial, var = "sizeRes",
                          before = c("capital, large city", "small city", "town"),
                          after = c("urban", "urban", "urban"))

# Recodificar rural
sdcInitial  <-  groupAndRename(obj = sdcInitial, var = c("sizeRes"),
                          before = c("countryside"), after = c("rural"))

# Frequencias de sizeRes después de recodificar
table(sdcInitial@manipKeyVars$sizeRes)

## 
## urban rural 
##  1316   684

La 8.1 ilustra el efecto de la recodificación de la variable “sizeRes” y muestra respectivamente los recuentos de frecuencia antes y después de la recodificación. Vemos que el número de categorías se ha reducido de 4 a 2 y las categorías pequeñas (“small city” y “town”) han desaparecido.

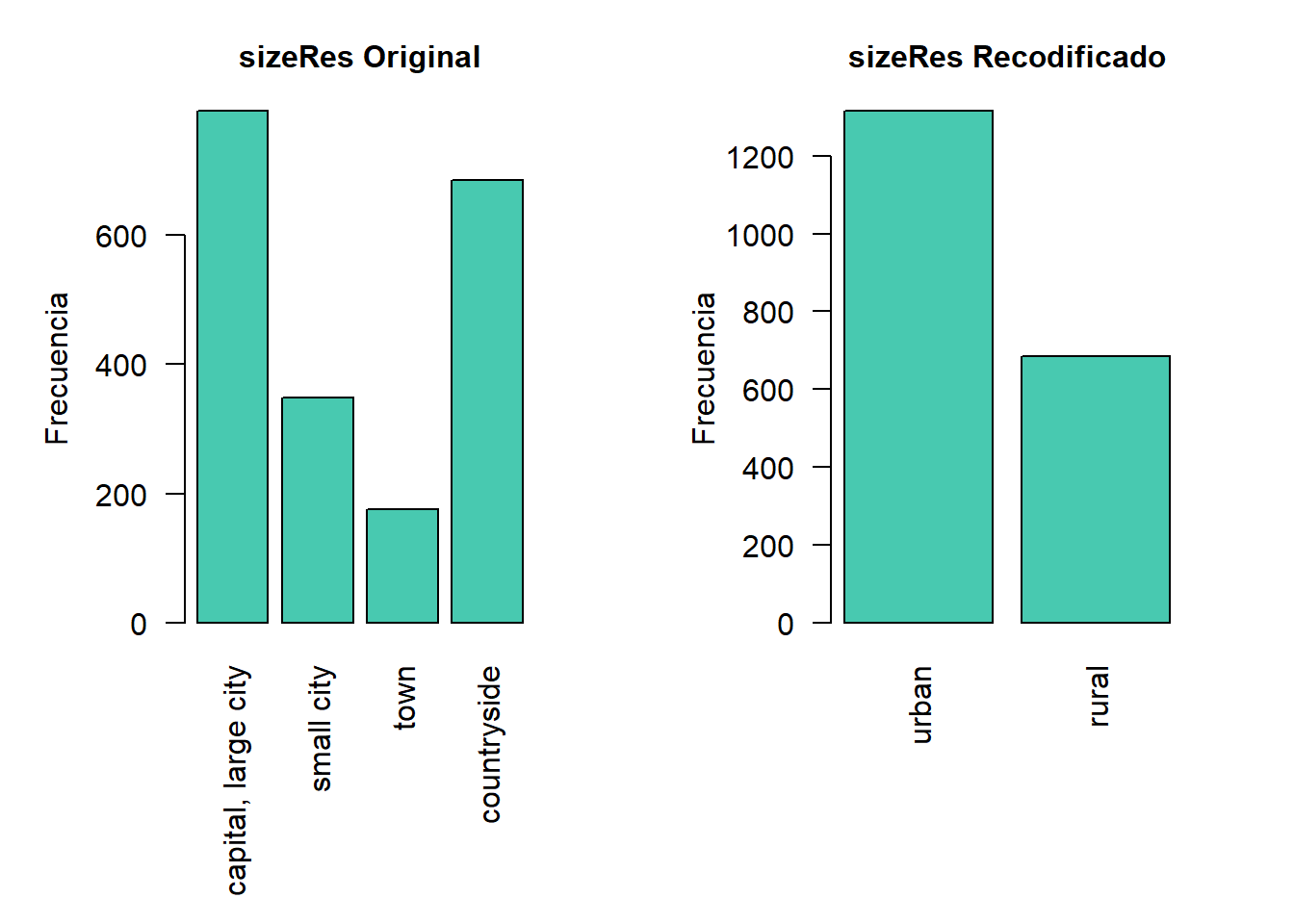
Figura 8.1: Efecto de la recodificación y recuentos de frecuencia antes y después de la recodificación

8.2.1.1.2 Recodificación de una variable continua mediante la función sdcMicro: globalRecode()

La recodificación global de las variables numéricas (continuas) puede lograrse en sdcMicro utilizando la función globalRecode(), que permite especificar un vector con los puntos de quiebre entre los intervalos. La recodificación de una variable continua la convierte en una variable categórica. Además, se puede especificar un vector de etiquetas para las nuevas categorías. Por defecto, las etiquetas son los intervalos, por ejemplo, “(0, 10]”. El Bloque 8.2 muestra cómo recodificar la variable edad en intervalos de 10 años para valores de edad entre 0 y 100.

Nota: A los valores que quedan fuera de los intervalos especificados se les asigna un valor perdido NA

Por lo tanto, los intervalos deben cubrir todo el rango de valores de la variable.

Bloque 8.2 Uso de la función sdcMicro globalRecode() para recodificar una variable continua (edad)

sdcInitial <- globalRecode(sdcInitial, column = c("AGEYRS"),
                           breaks = 10 * c(0:10))

# Frecuencias de edad después de recodificar
table(sdcInitial@manipKeyVars$AGEYRS)

## 
##   (0,10]  (10,20]  (20,30]  (30,40]  (40,50]  (50,60]  (60,70]  (70,80]  (80,90] (90,100] 
##        0       44      389      578      428      266      173       92       27        3

# Guardo objeto de edad en tramos para volver a utilizar en localSupresion
sdcInitial_edad <- sdcInitial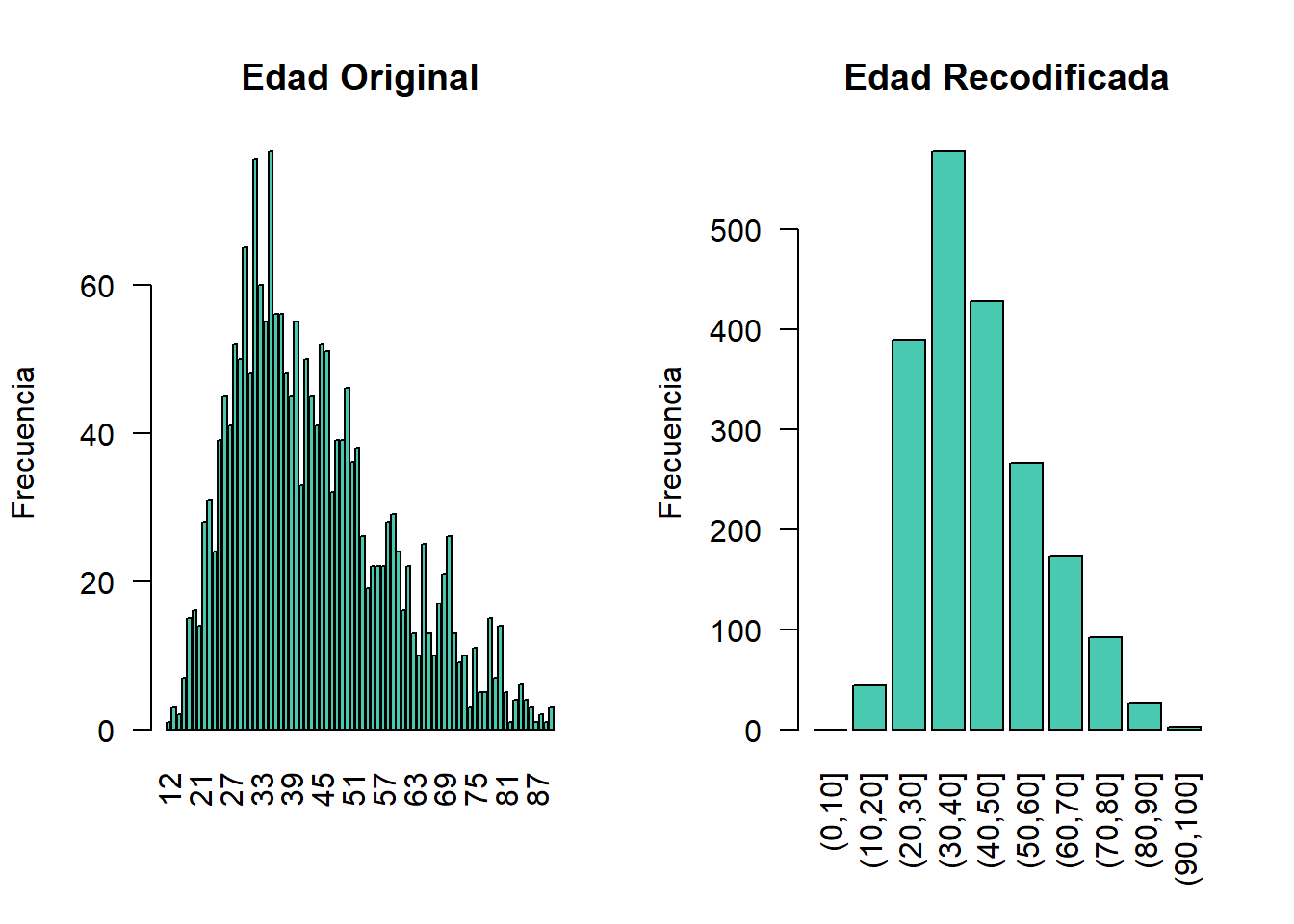

Figura 8.2: Variable de edad antes y después de la recodificación

En lugar de crear intervalos de igual anchura, también podemos crear intervalos de anchura desigual. Esto se ilustra en el Bloque 8.3, donde utilizamos los grupos de edad 1-5, 6-11, 12-17, 18-21, 22-25, 26-49, 50-64 y 65+. En este ejemplo, es un paso útil, ya que incluso después de recodificar en intervalos de 10 años, las categorías con valores de edad altos tienen frecuencias bajas. Elegimos los intervalos respetando los valores relevantes de la edad escolar y de la edad laboral (por ejemplo, la edad de jubilación es de 65 años en este ejemplo) de forma que los datos puedan seguir utilizándose para la investigación común sobre educación y empleo. La 8.3 muestra el efecto de la recodificación de la variable “edad”.

Bloque 8.3 Uso de globalRecode() para crear intervalos de ancho desigual

sdcInitial <- undolast(sdcInitial)

sdcInitial <- globalRecode(sdcInitial, column = c("AGEYRS"),
                           breaks = c(0, 5, 11, 17, 21, 25, 49, 65, 100))

# Frecuencias de edad después de recodificar
table(sdcInitial@manipKeyVars$AGEYRS)

## 
##    (0,5]   (5,11]  (11,17]  (17,21]  (21,25]  (25,49]  (49,65] (65,100] 
##        0        0        6       52      122     1213      398      209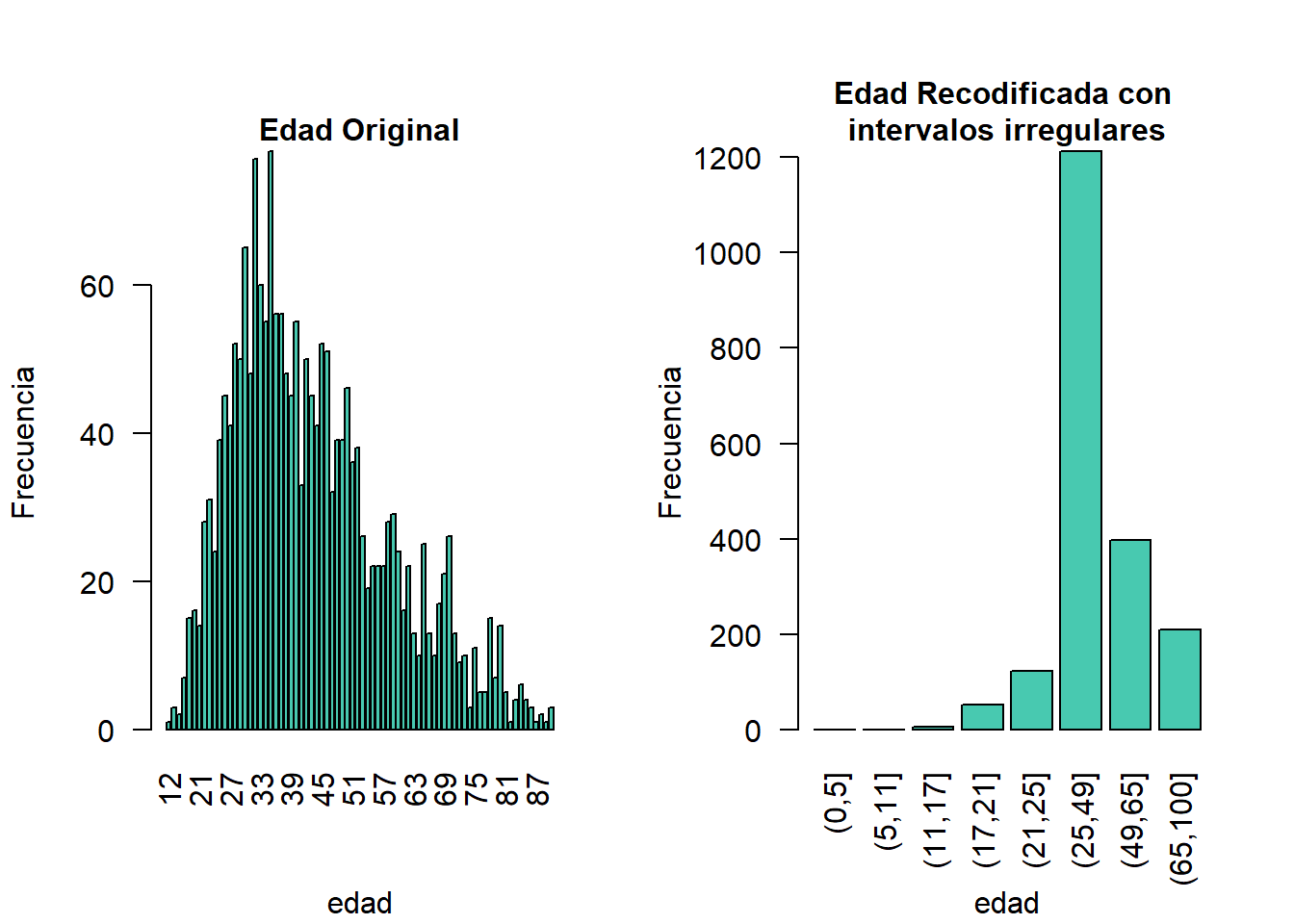

Figura 8.3: Variable de edad antes y después de la recodificación

Precaución sobre el uso de la función globalRecode() en sdcMicro: En la implementación actual de sdcMicro, los intervalos se definen como abiertos a la izquierda. En términos matemáticos, esto significa que, en nuestro ejemplo, la edad 0 está excluida de los intervalos especificados. En notación de intervalos, esto se denota como (0, 5] (como en las etiquetas del eje x en la 8.2 y la 8.3 para la variable recodificada). El intervalo (0, 5] se interpreta como de 0 a 5 y no incluye el 0, pero sí el 5. R recodifica los valores que no están contenidos en ninguno de los intervalos como perdidos (NA). Esta implementación establecería en nuestro ejemplo todos los valores de edad 0 (niños menores de 1 año) como perdidos y podría significar potencialmente una gran pérdida de datos. La función globalRecode() solo permite construir intervalos que queden abiertos. Este puede no ser un resultado deseable y la pérdida de las edades cero de los datos es claramente problemática para un conjunto de datos del mundo real.

Para construir intervalos abiertos a la derecha, por ejemplo, en nuestro ejemplo, para los intervalos de edad [0,14), [15, 65), [66, 100), presentamos dos alternativas de recodificación global:

• Una solución para las variables semicontinuas²¹ y el valor 9999,5 se clasificaría erróneamente como perteneciente al intervalo [10000, 19999].] que permitiría utilizar globalRecode() sería restar un pequeño número a los intervalos límite, permitiendo así crear los intervalos deseados. En el siguiente ejemplo, restar 0,1 a cada intervalo obliga a globalRecode() a incluir el 0 en el intervalo inferior y permitir las pausas donde las queramos. Establecemos el límite superior del intervalo para que sea mayor que el valor máximo de la variable “edad”. Podemos utilizar la opción etiquetas para definir etiquetas claras para las nuevas categorías. Esto se ilustra en el Bloque 8.4.

Bloque 8.4 Construcción de intervalos abiertos a la derecha para variables semicontinuas utilizando la función incorporada de sdcMicro, globalRecode()

sdcInitial <- undolast(sdcInitial)

sdcInitial <- globalRecode(sdcInitial, column = c("AGEYRS"),
                           breaks = c(-0.1, 14.9, 64.9, 99.9),
                           labels = c('[0,15)', '[15,65)', '[65,100)'))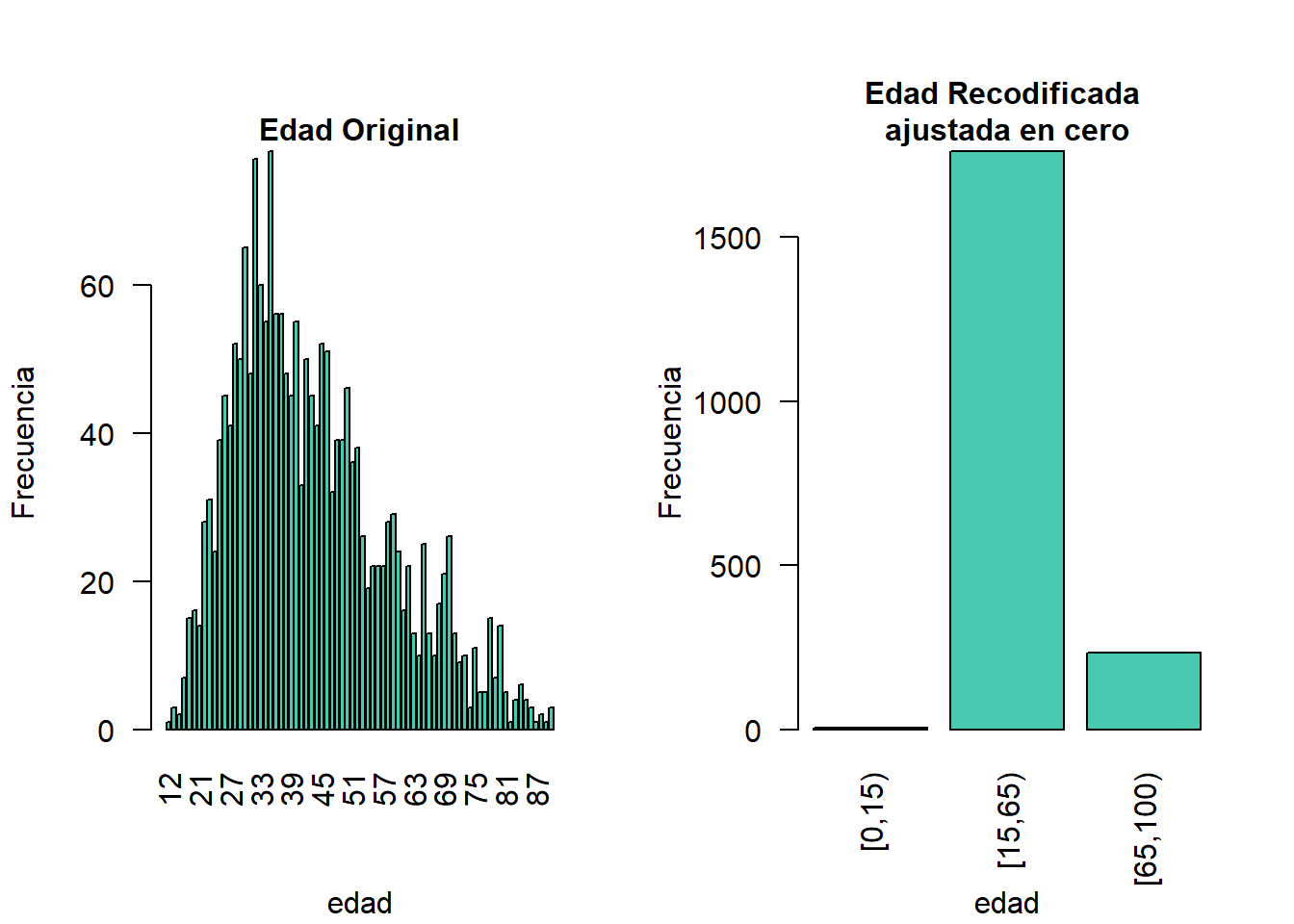

Figura 8.4: Variable de edad antes y después de la recodificación

• También es posible utilizar código en R para recodificar manualmente las variables sin utilizar las funciones sdcMicro. Cuando se utilizan las funciones sdcMicro, el cambio en el riesgo después de la recodificación se recalcula automáticamente, pero si se recodifica manualmente no lo hace. En este caso, hay que dar un paso más y recalcular el riesgo después de cambiar manualmente las variables en el objeto sdcMicro. Este enfoque también es válido para las variables continuas y se ilustra en el Bloque 8.5.

Bloque 8.5 Construcción de intervalos para variables semicontinuas y continuas mediante recodificación manual en R

sdcInitial <- undolast(sdcInitial)

# Grupo edad 0-14
sdcInitial@manipKeyVars$AGEYRS[sdcInitial@manipKeyVars$AGEYRS >= 0 &
sdcInitial@manipKeyVars$AGEYRS < 15] <- 0

# Grupo edad 15-64
sdcInitial@manipKeyVars$AGEYRS[sdcInitial@manipKeyVars$AGEYRS >= 15 &
sdcInitial@manipKeyVars$AGEYRS < 65] <- 1

# Grupo edad 65-100
sdcInitial@manipKeyVars$AGEYRS[sdcInitial@manipKeyVars$AGEYRS >= 65 &
sdcInitial@manipKeyVars$AGEYRS <= 100] <- 2

# Añadir etiquetas para los nuevos valores
sdcInitial@manipKeyVars$AGEYRS <-ordered(sdcInitial@manipKeyVars$AGEYRS,
levels = c(0,1,2), labels = c("0-14", "15-64", "65-100"))

# Recalcular el riesgo tras una transformación manual
sdcInitial <- calcRisks(sdcInitial)

8.2.1.2 Codificación superior e inferior

La codificación superior e inferior es similar a la recodificación global, pero en lugar de recodificar todos los valores, solo se recodifican los valores superiores y/o inferiores de la distribución o las categorías. Esto solo puede aplicarse a las variables categóricas ordinales y a las variables semi-continuas, ya que los valores tienen que estar al menos ordenados. La codificación superior e inferior es especialmente útil si el grueso de los valores se encuentra en el centro de la distribución y las categorías periféricas tienen pocas observaciones (valores atípicos). Los ejemplos son la edad y los ingresos; para estas variables, a menudo habrá solo unas pocas observaciones por encima de ciertos umbrales, normalmente en las colas de la distribución. Cuanto menor sea el número de observaciones dentro de una categoría, mayor será el riesgo de identificación. Una solución podría ser agrupar los valores de las colas de la distribución en una categoría. Esto reduce el riesgo para esas observaciones y, lo que es más importante, lo hace sin reducir la utilidad de los datos para las demás observaciones de la distribución.

Decidir dónde aplicar el umbral y qué observaciones deben agruparse requiere:

• Revisar la distribución global de la variable para identificar en qué punto las frecuencias caen por debajo del número deseado de observaciones e identificar los valores atípicos en la distribución. 8.5 muestra la distribución de la variable edad y sugiere 65 (línea vertical roja) para el código superior de edad.
• Tener en cuenta el uso previsto de los datos y el propósito para el que se realizó la encuesta. Por ejemplo, si los datos se utilizan normalmente para medir la participación en la fuerza laboral de las personas de 15 a 64 años, la codificación superior e inferior no debe interferir con las categorías de 15 a 64 años. De lo contrario, el analista se encontraría con la imposibilidad de crear las medidas deseadas para las que estaban destinados los datos. En el ejemplo, consideramos esto y codificamos todas las edades superiores a 64 años.

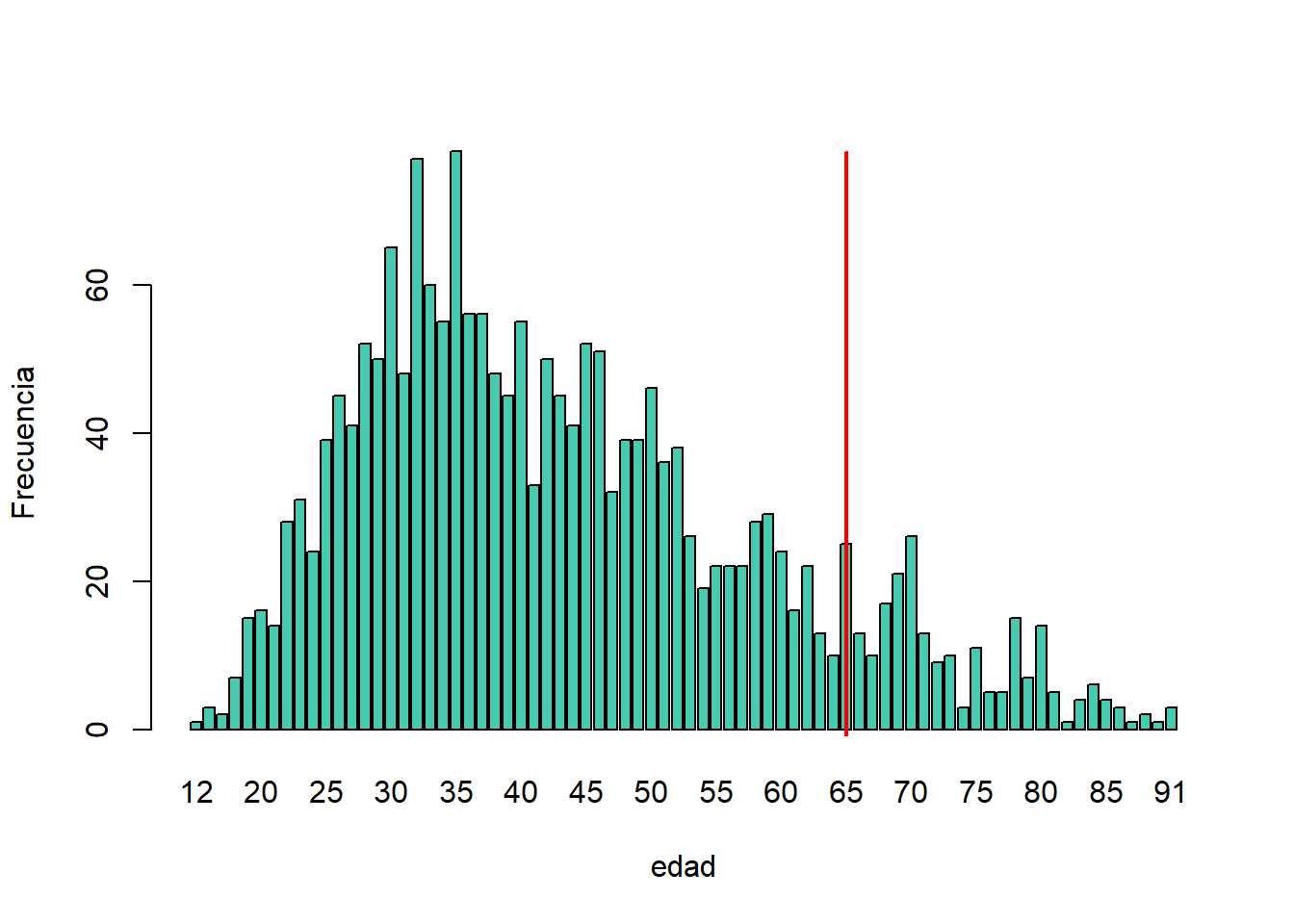
Figura 8.5: Utilización de la distribución de frecuencias de la variable edad para determinar el umbral de la codificación superior

La codificación superior e inferior se puede hacer fácilmente con la función topBotCoding() en sdcMicro. La codificación superior y la inferior no pueden hacerse simultáneamente en sdcMicro. El Bloque 8.6 ilustra cómo recodificar valores de edad superior a 64 y valores de edad inferior a 5; 65 y 5 reemplazan los valores respectivamente. Para construir varias categorías de codificación superior o inferior, por ejemplo, edad de 65 a 80 años y superior a 80 años, se puede utilizar la función groupAndRename() en sdcMicro o la recodificación manual como se describe en la subsección anterior.

Bloque 8.6 Codificación superior y codificación inferior en sdcMicro utilizando la función topBotCoding()

sdcInitial <- sdc_respaldo # leo nuevamente la Tabla

# Top coding en edad 65
sdcInitial <- topBotCoding(obj = sdcInitial, value = 65, replacement = 65,
                           kind = "top", column = "AGEYRS")

# Bottom coding en edad 5
sdcInitial <- topBotCoding(obj = sdcInitial, value = 5, replacement = 5,
                           kind = "bottom", column = "AGEYRS")

#table(sdcInitial@manipKeyVars$AGEYRS)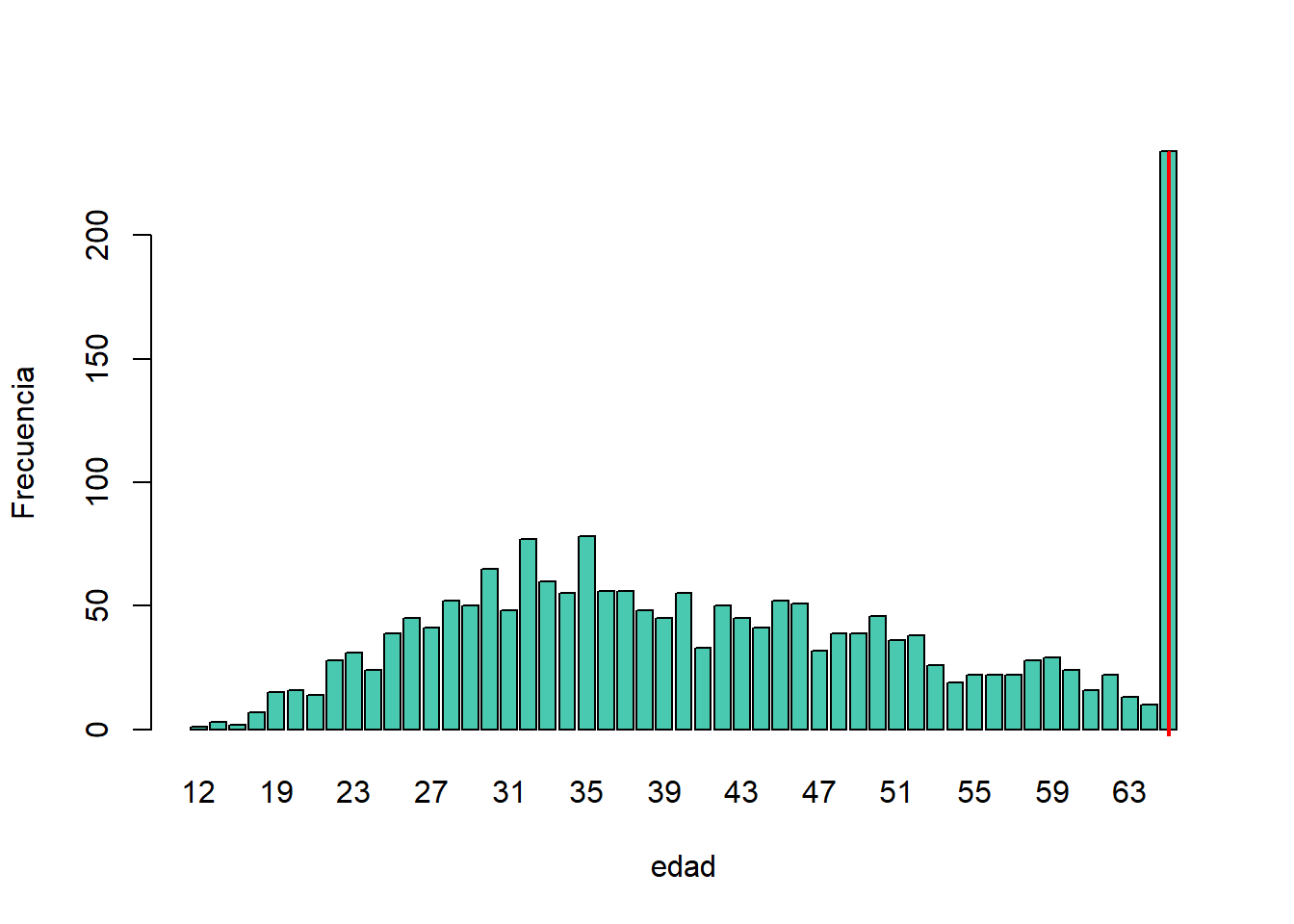

Figura 8.6: Distribución de frecuencias de la variable edad con codificación superior

8.2.1.3 Redondeo

El redondeo es similar a la agrupación, pero se utiliza para las variables continuas. El redondeo es útil para evitar la coincidencia exacta con fuentes de datos externas. Además, puede utilizarse para reducir el nivel de detalle de los datos. Algunos ejemplos son la eliminación de las cifras decimales o el redondeo a la unidad más cercana.

sdcInitial <- sdc_respaldo # leo nuevamente la Tabla

table(sdcInitial@manipKeyVars$AGEYRS)

## 
## 12 14 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 
##  1  3  2  7 15 16 14 28 31 24 39 45 41 52 50 65 48 77 60 55 78 56 56 48 45 55 33 50 45 41 52 
## 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 
## 51 32 39 39 46 36 38 26 19 22 22 22 28 29 24 16 22 13 10 25 13 10 17 21 26 13  9 10  3 11  5 
## 77 78 79 80 81 82 83 84 85 86 87 88 90 91 
##  5 15  7 14  5  1  4  6  4  3  1  2  1  3

# Se redondea a la decena más cercana
sdcInitial@manipKeyVars$AGEYRS <- round(sdcInitial@manipKeyVars$AGEYRS,-1)

table(sdcInitial@manipKeyVars$AGEYRS)

## 
##  10  20  30  40  50  60  70  80  90 
##   4 176 493 559 326 233 122  77  10

En la siguiente sección se analiza el método de supresión local. La recodificación suele utilizarse antes de la supresión local para reducir el número de supresiones necesarias.

Lectura recomendada de recodificación:
- Hundepool, Anco, Josep Domingo-Ferrer, Luisa Franconi, Sarah Giessing, Rainer Lenz, Jane Naylor, Eric Schulte Nordholt, Giovanni Seri, and Peter Paul de Wolf. 2006. Handbook on Statistical Disclosure Control. ESSNet SDC. http://neon.vb.cbs.nl/casc/handbook.htm.
- Hundepool, Anco, Josep Domingo-Ferrer, Luisa Franconi, Sarah Giessing, Eric Schulte Nordholt, Keith Spicer, and Peter Paul de Wolf. 2012. Statistical Disclosure Control. Chichester: John Wiley & Sons Ltd. doi:10.1002/9781118348239.
- Templ, Matthias, Bernhard Meindl, Alexander Kowarik, and Shuang Chen. 2014. Statistical Disclosure Control (SDCMicro). http://www.ihsn.org/home/software/disclosure-control-toolbox. (accessed June 9, 2018).
- De Waal, A.G., and Willenborg, L.C.R.J. 1999. Information loss through global recoding and local suppression. Netherlands Official Statistics, 14:17-20, 1999. Special issue on SDC

8.2.2 Supresión local

En las encuestas es frecuente encontrar valores para ciertas variables o combinaciones de identificadores indirectos que son compartidos por muy pocos individuos. Cuando esto ocurre, el riesgo de reidentificación para esos encuestados es mayor que para el resto de los encuestados (véase la sección k-anonimato). A menudo se utiliza la supresión local tras reducir el número de claves en los datos al recodificar las variables adecuadas. La recodificación reduce el número de supresiones necesarias, así como el tiempo de cálculo para la supresión. La supresión de valores significa que los valores de una variable se sustituyen por un valor ausente NA en R). En la sección k-anonimato se analiza cómo influyen los valores perdidos en los recuentos de frecuencia y en el \(k\)-anonimato. Es importante tener en cuenta que no se suprimen todos los valores de todos los individuos de una determinada variable, lo que ocurriría al eliminar un identificador directo, como el “nombre”; solo se suprimen determinados valores de una variable concreta y de un encuestado o conjunto de encuestados concreto. Esto se ilustra en el siguiente ejemplo y en la Tabla 8.4.

La Tabla 8.4 presenta un conjunto de datos con siete encuestados y tres identificadores indirectos. La combinación {“mujer”, “rural”, “superior”} para las variables “sexo”, “región” y “educación” es una combinación poco segura, ya que es única en la muestra. Al suprimir el valor “mujer” o “superior”, el encuestado ya no puede distinguirse de los demás encuestados, ya que ese encuestado comparte la misma combinación de variables clave con al menos otros tres encuestados. Solo se suprime el valor de la combinación insegura del único encuestado en riesgo, no los valores de la misma variable de los demás encuestados. La libertad de elegir qué valor se suprime puede utilizarse para minimizar el número total de supresiones y, por tanto, la pérdida de información. Además, si una variable es muy importante para el usuario, podemos elegir no suprimir los valores de esta variable, a menos que sea estrictamente necesario. En el ejemplo, podemos elegir entre suprimir el valor “mujer” o “mayor” para conseguir un archivo de datos seguro; elegimos suprimir “mayor”. Esta elección debe hacerse teniendo en cuenta las necesidades de los usuarios de los datos. En este ejemplo, consideramos que “sexo” es más importante que “educación”.

Tabla 8.4: Ilustración de la supresión local - datos antes y después de la supresión

Datos originales				Después de supresión local
ID	Sexo	Zona	Educación	Sexo	Zona	Educación
1	mujer	rural	superior	mujer	rural	NA / perdido
2	hombre	rural	superior	hombre	rural	superior
3	hombre	rural	superior	hombre	rural	superior
4	hombre	rural	superior	hombre	rural	superior
5	mujer	rural	media	mujer	rural	media
6	mujer	rural	media	mujer	rural	media
7	mujer	rural	media	mujer	rural	media

Dado que las variables continuas tienen un elevado número de valores únicos (por ejemplo, los ingresos en dólares o la edad en años), el \(k\)-anonimato y la supresión local no son adecuadas para las variables continuas o las variables con un número muy elevado de categorías. Una posible solución en esos casos podría ser recodificar primero para producir menos categorías (por ejemplo, recodificar la edad en intervalos de 10 años o los ingresos en quintiles). No obstante, tenga siempre presente el efecto que tendrá cualquier recodificación en la utilidad de los datos.

El paquete sdcMicro incluye dos funciones para la supresión local: localSuppression() y localSupp(). La función localSuppression() es la más utilizada y permite el uso de la supresión en identificadores indirectos especificados para lograr un cierto nivel de \(k\)-anonimato para estos identificadores indirectos. El algoritmo utilizado busca minimizar el número total de supresiones mientras se alcanza el umbral de \(k\)-anonimato requerido. Por defecto, el algoritmo tiene más probabilidades de suprimir valores de variables con muchas categorías o valores diferentes, y menos de suprimir variables con menos categorías. Por ejemplo, es más probable que se supriman los valores de una variable geográfica, con 12 áreas diferentes, que los valores de la variable “sexo”, que suele tener solo dos categorías. Si las variables con muchos valores diferentes son importantes para la utilidad de los datos y no se desea la supresión para ellas, es posible clasificar las variables por importancia en la función localSuppression() y así especificar el orden en el que el algoritmo tratará de suprimir los valores dentro de los identificadores indirectos para lograr el \(k\)-anonimato. El algoritmo trata de aplicar menos supresiones a las variables de gran importancia que a las de menor importancia. Sin embargo, las supresiones en las variables con alta importancia pueden ser inevitables para lograr el nivel requerido de \(k\)-anonimato.

En el Bloque 8.7, se aplica la supresión local para alcanzar el umbral de \(k\)-anonimato de 5 en los identificadores indirectos “sexo”, “región”, “religión”, “edad” y “etnia”²². Sin clasificar la importancia de las variables, el valor de la variable “edad” es más probable que se suprima, ya que es la variable con más categorías. La variable “edad” tiene 10 categorías después de la recodificación. La variable “sexo” es la menos probable que se suprima, ya que solo tiene dos valores diferentes: “hombre” y “mujer”. Las demás variables tienen 4 categorías (“tamañoRes”), 2 (“región”) y 8 (“etnia”). Después de aplicar la función localSuppression(), mostramos el número de supresiones por variable con la función incorporada print() con la opción ‘ls’ para la salida de supresión local. Como se esperaba, la variable “edad” es la que tiene más supresiones (80). De hecho, solo la variable “etnia” de las demás variables también necesitó supresiones (8) para alcanzar el umbral de \(k\)-anonimato de 5. La variable “etnia” es la segunda variable con mayor número de supresiones. Posteriormente, deshacemos y rehacemos la supresión local en los mismos datos y reducimos el número de supresiones en “edad” especificando el vector de importancia con alta importancia (poca supresión) en el identificador indirecto “edad”. También,asignamos importancia a la variable “sexo”. Esto se hace especificando un vector de importancia. Los valores del vector de importancia pueden ir de 1 a k, el número de identificadores indirectos. En nuestro ejemplo, k es igual a 5. Las variables con valores más bajos en los vectores de importancia tienen una importancia alta y, cuando es posible, reciben menos supresiones que las variables con valores más altos.

Para asignar una importancia alta a las variables “edad” y “sexo”, especificamos el vector de importancia como c(5, 1, 1, 4, 4, 5), con el orden según el orden de las variables especificadas en el objeto sdcMicro. El efecto es claro: no hay supresiones en las variables “edad” y “sexo”. En cambio, las demás variables, especialmente “tamañoRes” y “etnia”, recibieron muchas más supresiones. El número total de valores suprimidos ha aumentado de 88 a 166.

Nota: Un menor número de supresiones en una variable aumenta el número de supresiones necesarias en otras variables (véase el Bloque 8.7).

Por lo general, el número total de valores suprimidos necesarios para alcanzar el nivel requerido de \(k\)-anonimato aumenta cuando se especifica un vector de importancia, ya que el vector de importancia impide utilizar el patrón de supresión óptimo. El vector de importancia debe especificarse solo en los casos en que las variables con muchas categorías desempeñen un papel importante en la utilidad de los datos para los usuarios de los mismos²³.

Bloque 8.7 Aplicación de la supresión local con y sin vector de importancia

# Se comienza con la edad recodificada en tramos de 10 años
sdcInitial <- sdcInitial_edad
#sdcInitial <- sdc_respaldo # leo nuevamente la Tabla
#sdcInitial <- undolast(sdcInitial)

# supresión local sin vector de importancia
sdcInitial <- localSuppression(sdcInitial, k = 2)
print(sdcInitial, type="ls")

## Local suppression (applied per strata given by variable(s) strata_region)

##   KeyVar | Suppressions (#) | Suppressions (%)
##  sizeRes |                1 |            0.050
##   AGEYRS |              280 |           14.000
##   GENDER |                0 |            0.000
##   REGION |                0 |            0.000
##    etnia |               17 |            0.850
##    RELIG |               25 |            1.250

## ----------------------------------------------------------------------

# Deshacer las supresiones
sdcInitial <- undolast(sdcInitial)

# Supresión local con vector de importancia para evitar supresiones
# en las variables primera (sexo) y cuarta (edad)

sdcInitial <- localSuppression(sdcInitial, importance = c(5, 1, 1, 4, 4, 5), k = 2) #  c(5, 1, 1, 5, 5), k = 5)
print(sdcInitial, type="ls")

## Local suppression (applied per strata given by variable(s) strata_region)

##   KeyVar | Suppressions (#) | Suppressions (%)
##  sizeRes |              138 |            6.900
##   AGEYRS |               16 |            0.800
##   GENDER |                1 |            0.050
##   REGION |                0 |            0.000
##    etnia |              108 |            5.400
##    RELIG |               60 |            3.000

## ----------------------------------------------------------------------

La 8.7 demuestra el efecto del umbral de \(k\)-anonimato requerido y el vector de importancia en la utilidad de los datos utilizando varios indicadores relacionados con el mercado laboral de un conjunto de datos²⁴ antes y después de la anonimización. La 8.7 muestra los cambios relativos como porcentaje del valor inicial después de volver a calcular los indicadores con los datos a los que se aplicó la supresión local. Los indicadores son la proporción de mujeres y hombres activos y el número de mujeres y hombres en edad de trabajar. Los valores calculados a partir de los datos brutos son, respectivamente, 68%, 12%, 8.943 y 9.702. La línea vertical en 0 es el punto de referencia de la ausencia de cambios. Los números indican el umbral de \(k\)-anonimato requerido (3 o 5) y los colores indican el vector de importancia: el rojo (sin símbolo) es ningún vector de importancia, el azul (con símbolo \(\color {blue}{\text{*}}\)) es de alta importancia en la variable con la información sobre la situación laboral y el verde oscuro (con símbolo \(\color {darkgreen}{\text{+}}\)) es de alta importancia en la variable de edad.

Un umbral de \(k\)-anonimato más alto conlleva una mayor pérdida de información (es decir, mayores desviaciones de los valores originales de los indicadores, los 5 están más alejados del punto de referencia de ningún cambio que los correspondientes 3) causada por la supresión local. Reducir el número de supresiones en la variable de situación laboral especificando un vector de importancia no mejora los indicadores. En cambio, reducir el número de supresiones en la edad reduce en gran medida la pérdida de información. Dado que los grupos de edad específicos tienen una gran influencia en el cálculo de estos indicadores (los casos raros se encuentran en los extremos y se suprimirán), los índices de supresión elevados sobre la edad distorsionan los indicadores. En general, es útil comparar las medidas de utilidad (véase la sección Medición de la utilidad y la pérdida de información) para especificar el vector de importancia, ya que los efectos pueden ser imprevisibles.

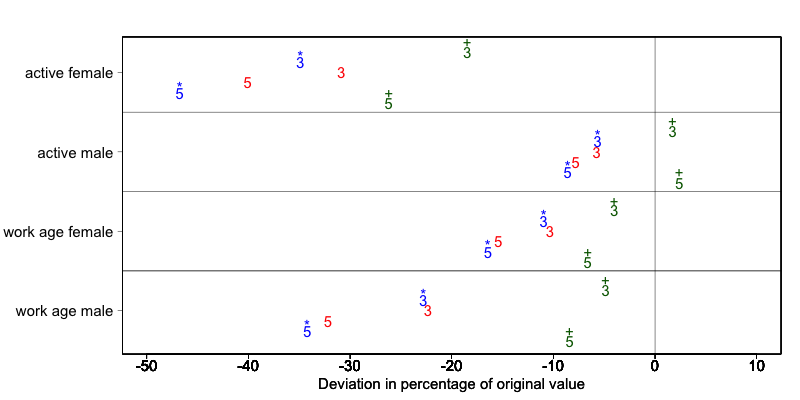
Figura 8.7: Cambios en los indicadores del mercado laboral tras la anonimización de los datos de I2D2

El umbral de \(k\)-anonimato que debe fijarse depende de varios factores, que son, entre otros:

1. Los requisitos legales para un archivo de datos seguro.
2. Otros métodos que se aplicarán a los datos.
3. El número de supresiones y la consiguiente pérdida de información resultante de umbrales más altos.
4. El tipo de variable.
5. Las ponderaciones y el tamaño de la muestra.
6. El tipo de publicación (véase la sección Tipos de liberación de datos).

Los niveles aplicados habitualmente para el umbral de \(k\)-anonimato son 3 y 5.

La Tabla 8.5 ilustra la influencia del vector de importancia y el umbral de \(k\)-anonimato en el tiempo de ejecución, el riesgo global tras la supresión y el número total de supresiones necesarias para alcanzar este umbral de \(k\)-anonimato. El conjunto de datos contiene unos 63.000 individuos. Cuanto mayor sea el umbral de \(k\)-anonimato, más supresiones serán necesarias y menor será el riesgo tras la supresión local (número esperado de reidentificaciones). En este ejemplo concreto, el tiempo de cálculo es menor para los umbrales más altos. Esto se debe al mayor número de supresiones necesarias, lo que reduce la dificultad de la búsqueda de un patrón de supresión óptimo.

La variable edad se recodifica en intervalos de cinco años y tiene 20 categorías de edad. Esta es la variable con el mayor número de categorías. Dar prioridad a la supresión de otras variables conduce a un mayor número total de supresiones y a un mayor tiempo de cálculo.

Tabla 8.5: Efecto de los vectores de importancia y umbrales de \(k\)-anonimato en el tiempo de ejecución y número total de supresiones

Umbral k-anonimato	Vector de importancia	Número total de supresiones	Umbral k-anonimato	Vector de importancia	Número total de supresiones
3	ninguno (por defecto)	6,676	5,387	293.0	11.8
3	situación laboral	7,254	5,512	356.5	13.1
3	variable de edad	8,175	60	224.6	4.5
5	ninguno (por defecto)	9,971	7,894	164.6	8.5
5	situación laboral	11,668	8,469	217.0	10.2
5	variable de edad	13,368	58	123.1	3.8

En los casos en que hay un gran número de identificadores indirectos y las variables tienen muchas categorías, el número de combinaciones posibles aumenta rápidamente (véase k-anonimato). Si el número de variables y categorías es muy grande, el tiempo de cálculo del algoritmo localSuppression() puede ser muy largo (véase la sección Tiempo de cómputo sobre el tiempo de cálculo). Además, es posible que el algoritmo no llegue a una solución, o que llegue a una solución que no cumpla el nivel de \(k\)-anonimato especificado. Por lo tanto, se recomienda reducir el número de identificadores indirectos y/o categorías antes de aplicar la supresión local. Esto puede hacerse recodificando las variables o seleccionando algunas variables para otros métodos (perturbativos), como el PRAM. De este modo se garantiza que el número de supresiones sea limitado y, por tanto, la pérdida de datos se limite solo a los valores que suponen un mayor riesgo.

En algunos conjuntos de datos, puede resultar difícil reducir el número de identificadores indirectos e incluso después de reducir el número de categorías mediante recodificación, el algoritmo de supresión local tarda mucho tiempo en calcular las supresiones necesarias. Una solución en estos casos puede ser el llamado “enfoque all-m” (véase (Wolf 2015)). El enfoque all-m consiste en aplicar el algoritmo de supresión local descrito anteriormente a todos los posibles subconjuntos de tamaño m del conjunto total de identificadores indirectos. La ventaja de este enfoque es que los problemas parciales son más fáciles de resolver y el tiempo de cálculo será menor. Hay que tener cuidado, ya que este método no conduce necesariamente al \(k\)-anonimato en el conjunto completo de identificadores indirectos. Hay dos posibilidades para alcanzar el mismo nivel de protección 1) elegir un umbral más alto para k o 2) volver a aplicar el algoritmo de supresión local en el conjunto completo de k después de utilizar el método all-m para alcanzar el umbral requerido. En el segundo caso, el enfoque all-m conduce a un menor tiempo de cálculo a costa de un mayor número total de supresiones.

Nota: El nivel requerido no se alcanza automáticamente en todo el conjunto de identificadores indirectos si se utiliza el enfoque all-m.

Por lo tanto, es importante evaluar cuidadosamente las medidas de riesgo después de utilizar el enfoque all-m.

En sdcMicro el enfoque all-m se implementa en el argumento ‘combs’ de la función localSuppression(). El valor de m se especifica en el argumento ‘combs’ y también puede tomar varios valores. Los subconjuntos de diferentes tamaños se utilizan secuencialmente en el algoritmo de supresión local. Por ejemplo, si ‘combs’ se establece como c(3,9), primero se consideran todos los subconjuntos de tamaño 3 y posteriormente todos los subconjuntos de tamaño 9. Establecer el último valor del argumento combs en el número total de variables clave garantiza la consecución del \(k\)-anonimato para el conjunto de datos completo. También es posible especificar diferentes valores de k para cada tamaño de subconjunto en el argumento k. Si quisiéramos lograr el anonimato de 5 en los subconjuntos de tamaño 3 y posteriormente el anonimato de 3 en los subconjuntos de tamaño 9, estableceríamos el argumento k como c(5,3). El Bloque 8.8 ilustra el uso del enfoque all-m en sdcMicro.

Bloque 8.8 El enfoque all-m en sdcMicro

sdcInitial <- undolast(sdcInitial)

# Aplicar k-anonimato con umbral 5 a todos los subconjuntos de dos variables clave y
# posteriormente al conjunto de datos completo
sdcInitial <- localSuppression(sdcInitial, k = 5, combs = c(2, 5))
print(sdcInitial, type="ls")

## Local suppression (applied per strata given by variable(s) strata_region)

##   KeyVar | Suppressions (#) | Suppressions (%)
##  sizeRes |                0 |            0.000
##   AGEYRS |              510 |           25.500
##   GENDER |                0 |            0.000
##   REGION |                0 |            0.000
##    etnia |               82 |            4.100
##    RELIG |               52 |            2.600

## ----------------------------------------------------------------------

sdcInitial <- undolast(sdcInitial)
# Aplicar k-anonimato con umbral 5 a todos los subconjuntos de tres variables clave y
# posteriormente con el umbral 2 al conjunto de datos completo
sdcInitial <- localSuppression(sdcInitial, k = c(3, 5), combs = c(5, 2))
print(sdcInitial, type="ls")

## Local suppression (applied per strata given by variable(s) strata_region)

##   KeyVar | Suppressions (#) | Suppressions (%)
##  sizeRes |                0 |            0.000
##   AGEYRS |              409 |           20.450
##   GENDER |                0 |            0.000
##   REGION |                0 |            0.000
##    etnia |               34 |            1.700
##    RELIG |               52 |            2.600

## ----------------------------------------------------------------------

La Tabla 8.6 presenta los resultados de utilizar el enfoque all-m de un conjunto de datos de prueba con 9 variables clave y 4.000 registros. La Tabla muestra los argumentos k y “combs” de la función localSuppression(), el número de violaciones de \(k\)-anonimato para diferentes niveles de k, así como el número total de supresiones. Observamos que las diferentes combinaciones no siempre conducen al nivel de \(k\)-anonimato requerido. Por ejemplo, cuando se establece k=3, y “combs” 3 y 7, todavía hay 15 registros en el conjunto de datos (con un total de 9 identificadores indirectos) que violan el anonimato 3 después de la supresión local. Debido al menor tamaño de la muestra, las ganancias en tiempo de ejecución no son todavía evidentes en este ejemplo, ya que la ejecución del algoritmo varias veces consume tiempo. Un conjunto de datos más grande se beneficiaría más del enfoque all-m, ya que el algoritmo tardaría más tiempo.

Tabla 8.6: Efecto del enfoque all-m en el \(k\)-anonimato

Argumentos		Número de incumplimientos para diferentes niveles de \(k\)-anonimato en el conjunto completo			Número total de supresiones	Tiempo de ejecución (segundos)
k	combs	k = 2	k = 3	k = 5	.	.
Antes supresión	de la local	2,464	3,324	3,877	0	0.00
3	.	0	0	1,766	2,264	17.08
5	.	0	0	0	3,318	10.57
3	3	2,226	3,202	3,819	3,873	13.39
3	3,7	15	108	1,831	6,164	46.84
3	3,9	0	0	1,794	5,982	31.38
3	5,9	0	0	1,734	6,144	62.30
5	3	2,047	3,043	3,769	3,966	12.88
5	3,7	0	6	86	7,112	46.57
5	3,9	0	0	0	7,049	24.13
5	5,9	0	0	0	7,129	54.76
5,3	3,7	11	108	1,859	6,140	45.60
5,3	3,9	0	0	1,766	2,264	30.07
5,3	5,9	0	0	0	3,318	51.25

A menudo el conjunto de datos contiene variables relacionadas con las variables clave utilizadas para la supresión local. Ejemplos de ello son las variables rural/urbano a las regiones en caso de que las regiones sean completamente rurales o urbanas o las variables que solo se responden para categorías específicas (por ejemplo, el sector para los que trabajan, las variables relacionadas con la escolaridad para ciertos rangos de edad). En esos casos, las variables rural/urbana o sector podrían no ser identificadores indirectos en sí mismas, pero podrían permitir al intruso reconstruir valores suprimidos en los identificadores indirectos región o situación laboral. Por ejemplo, si la región 1 es completamente urbana y todas las demás regiones son solo semiurbanas o rurales, una supresión en la variable región para un registro de la región 1 puede reconstruirse simplemente mediante la variable rural/urbana. Por lo tanto, es útil suprimir los valores correspondientes a las supresiones en esas variables vinculadas. El Bloque 8.9 ilustra cómo suprimir los valores de la variable “urbrur” correspondientes a las supresiones en la variable región. Todos los valores de “urbrur” que corresponden a un valor suprimido NA en la variable “region” se suprimen (se ponen a NA).

Bloque 8.9 Suprimir manualmente los valores de las variables vinculadas.

# Suprimir los valores de urbrur en el archivo si la región está suprimida
file[is.na(sdcInitial@manipKeyVars$region) &
    !is.na(sdcInitial@origData$region),'sizRes'] <- NA

Como alternativa, las variables vinculadas pueden especificarse al crear el objeto sdcMicro. Las variables vinculadas se denominan variables “fantasma”. Cualquier supresión en la variable clave conducirá a una supresión en las variables vinculadas a esa variable clave. El Bloque 8.10 muestra cómo especificar la vinculación entre “región” y “urbrur” con variables fantasma.

Bloque 8.10 Suprimir valores en variables enlazadas especificando variables fantasma

# Las variables fantasma (vinculadas) se especifican como una lista de vínculos
ghostVars <- list()

# Cada enlace es una lista, con la variable clave en el primer elemento y
# la(s) variable(s) vinculada(s) en el segundo elemento
ghostVars[[1]] <- list()
ghostVars[[1]][[1]] <- "REGION"
ghostVars[[1]][[2]] <- c("URBRUR")

# Crear sdcMicroObj

sdcInitial <- createSdcObj(dat=fileHH, keyVars=selectedKeyVarsHH, pramVars=pramVarsHH, weightVar=weightVarHH, numVars = numVarsHH, ghostVars = ghostVars)

# Las variables fantasma manipuladas se encuentran en manipGhostVars
head(sdcInitial@manipGhostVars,10)

##    URBRUR
## 1       2
## 8       1
## 12      2
## 20      1
## 31      2
## 38      1
## 42      1
## 44      1
## 46      2
## 47      1

La alternativa más sencilla para la función localSuppression() en sdcMicro es la función localSupp(). La función localSupp() puede utilizarse para suprimir los valores de ciertas variables clave de los individuos con riesgos superiores a un determinado umbral. En este caso, se suprimirán todos los valores de la variable especificada para los encuestados con un riesgo superior al umbral especificado. La medida de riesgo utilizada es el riesgo individual (véase la sección Riesgo individual. Esto es útil si una variable tiene valores sensibles que no deben publicarse para los individuos con alto riesgo de reidentificación. Lo que se considera alta probabilidad de reidentificación depende de los requisitos legales. En el siguiente ejemplo, los valores de la variable “educación” se suprimen para todos los individuos cuyo riesgo individual es superior a 0,08, lo que se ilustra en el Bloque 8.11. Para obtener una visión general de los valores de riesgo individuales, puede ser útil observar las estadísticas resumidas de los valores de riesgo individuales, así como el número de supresiones.

Bloque 8.11 Aplicación de la función integrada sdcMicro localSupp()

# Estadísticas resumidas
summary(sdcInitial@risk$individual[,1])

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 3.371e-05 7.124e-04 3.004e-03 4.893e-03 6.236e-03 8.541e-02

# Número de individuos con riesgo individual superior al 0,1
sum(sdcInitial@risk$individual[,1] > 0.08)

## [1] 2

# supresión local
sdcInitial <- localSupp(sdcInitial, threshold = 0.08, keyVar = "etnia")

print(sdcInitial, type="ls")

## Local suppression:

##   KeyVar | Suppressions (#) | Suppressions (%)
##  sizeRes |                0 |            0.000
##   AGEYRS |                0 |            0.000
##   GENDER |                0 |            0.000
##   REGION |                0 |            0.000
##    etnia |                2 |            0.100
##    RELIG |                0 |            0.000

## ----------------------------------------------------------------------

8.3 Métodos perturbativos

Los métodos perturbativos no suprimen los valores del conjunto de datos, sino que perturban (alteran) los valores para limitar el riesgo de divulgación creando incertidumbre en torno a los valores reales. Un intruso no sabe si una coincidencia entre los microdatos y un archivo externo es correcta o no. La mayoría de los métodos perturbativos se basan en el principio del enmascaramiento matricial, es decir, el conjunto de datos alterado \(Z\) se calcula como

\[Z = AXB + C\]

donde \(X\) son los datos originales, \(A\) es una matriz utilizada para transformar los registros, \(B\) es una matriz para transformar las variables y \(C\) es una matriz con ruido aditivo.

Nota: Las medidas de riesgo basadas en el recuento de frecuencias de las claves dejan de ser válidas tras aplicar los métodos perturbativos.

Esto puede verse en la Tabla 8.7, que muestra los mismos datos antes y después de intercambiar algunos valores. Los valores intercambiados aparecen en cursiva. Tanto antes como después de perturbar los datos, todas las observaciones violan el \(k\)-anonimato en el nivel 3 (es decir, cada clave no aparece más de dos veces en el conjunto de datos). No obstante, el riesgo de reidentificación correcta de los registros se reduce y, por tanto, es posible que no se revele la información contenida en otras variables (sensibles). Con cierta probabilidad, una coincidencia de los microdatos con un archivo de datos externo será errónea. Por ejemplo, un intruso encontraría un individuo con la combinación {“hombre”, “urbano”, “superior”}, que es una muestra única. Sin embargo, esta coincidencia no es correcta, ya que el conjunto de datos original no contenía ningún individuo con estas características y, por tanto, el individuo coincidente no puede ser una coincidencia correcta. El intruso no puede saber con certeza si la información revelada de otras variables para ese registro es correcta.

Tabla 8.7: Efecto del enfoque all-m en el \(k\)-anonimato

Variable	Datos originales			Después de perturbar los datos
ID	Sexo	Zona	Educación	Sexo	Zona	Educación
1	mujer	rural	superior	mujer	rural	superior
2	mujer	rural	superior	mujer	rural	media
3	hombre	rural	media	hombre	rural	media
4	hombre	rural	media	mujer	rural	media
5	mujer	urbana	media	hombre	urbana	superior
6	mujer	urbana	media	mujer	urbana	media

Una de las ventajas de los métodos perturbativos es que se reduce la pérdida de información, ya que no se suprimirán valores, dependiendo del nivel de perturbación. Una desventaja es que los usuarios de los datos pueden tener la impresión de que los datos no se han anonimizado antes de su publicación y estarán menos dispuestos a participar en futuras encuestas. Por lo tanto, es necesario elaborar informes tanto para uso interno como externo (véase Etapa 6.4.5: Generar reportes y liberar datos).

Una alternativa a los métodos perturbativos es la generación de archivos de datos sintéticos con las mismas características que los archivos de datos originales. Los archivos de datos sintéticos no se discuten en estas directrices. Aquí abordamos cinco métodos perturbativos: El método de post aleatorización (PRAM), la microagregación, la adición de ruido, el shuffling y el rank swapping.

8.3.1 PRAM (Método de Post-Aleatorización)

PRAM es un método perturbativo para datos categóricos. Este método reclasifica los valores de una o más variables, de manera que los intrusos que intentan reidentificar a los individuos en los datos lo hacen, sin embargo, con probabilidad positiva, la reidentificación realizada es con el individuo equivocado. Esto significa que el intruso puede ser capaz de hacer coincidir varios individuos entre los archivos externos y los archivos de datos liberados, pero no puede estar seguro de que estas coincidencias correspondan al individuo correcto.

PRAM se define mediante la matriz de transición \(P\), que especifica las probabilidades de transición, es decir, la probabilidad de que un valor de una determinada variable permanezca inalterado o se cambie a cualquiera de los otros \(k-1\) valores. \(k\) es el número de categorías o niveles del factor dentro de la variable que se va a PRAM. Por ejemplo, si la variable región tiene 10 regiones diferentes, \(k\) es igual a 10. En el caso de PRAM para una sola variable, la matriz de transición es de tamaño \(k∗k\). Ilustramos el PRAM con un ejemplo de la variable “región”, que tiene tres valores diferentes: “capital”, “rural1” y “rural2”. La matriz de transición para aplicar PRAM a esta variable es de tamaño 3*3:

\[\begin{split} P = \begin{bmatrix} 1 & 0 & 0 \\ 0.05 & 0.8 & 0.15 \\ 0.05 & 0.15 & 0.8 \\ \end{bmatrix} \end{split}\]

Los valores de la diagonal son las probabilidades de que un valor de la categoría correspondiente no se modifique. El valor 1 en la posición (1,1) de la matriz significa que todos los valores “capital” permanecen “capital”; esto podría ser una decisión útil, ya que la mayoría de los individuos viven en la capital y no necesitan protección. El valor 0,8 en la posición (2,2) significa que un individuo con valor “rural1” se quedará con probabilidad 0,8 “rural1”. Los valores 0,05 y 0,15 en la segunda fila de la matriz indican que el valor “rural1” se cambiará a “capital” o “rural2” con una probabilidad de 0,05 y 0,15, respectivamente. Si en el fichero inicial teníamos 5.000 individuos con valor “capital” y respectivamente 500 y 400 con valores “rural1” y “rural2”, esperamos después de aplicar PRAM tener 5.045 individuos con capital, 460 con rural1 y 395 con rural2 [9]. La recodificación se realiza de forma independiente para cada individuo. Vemos que la tabulación de la variable “región” arroja resultados diferentes antes y después de PRAM, que se muestran en la Tabla 8.8. La desviación de la expectativa se debe a que PRAM es un método probabilístico, es decir, los resultados dependen de un mecanismo de generación de probabilidades; en consecuencia, los resultados pueden diferir cada vez que aplicamos PRAM a las mismas variables de un conjunto de datos.

Nota:El número de valores modificados es mayor de lo que podría pensarse al inspeccionar las tabulaciones de la Tabla 8.8. No todos los 5.000 individuos con valor “capital” después de PRAM tenían este valor antes de PRAM y los 457 individuos en rural1 después de PRAM no están todos incluidos en los 500 individuos antes de PRAM. El número de cambios es mayor que las diferencias en la tabulación (véase la matriz de transición).

Dado que la matriz de transición es conocida por los usuarios finales, hay varias formas de corregir el análisis estadístico de los datos por las distorsiones introducidas por el PRAM.

Tabla 8.8: Tabulación de la variable “región” antes y después del PRAM

Valor	Tabulación antes de PRAM	Tabulación después de PRAM
rural1	500	457
rural2	400	391

Una forma de garantizar la consistencia entre las tabulaciones antes y después de PRAM es elegir la matriz de transición de forma que, en la expectativa, las tabulaciones antes y después de aplicar PRAM sean las mismas para todas las variables. [10] Este método se llama PRAM invariante y se implementa en sdcMicro en la función pram(). El método pram() determina la matriz de transición que satisface los requisitos de PRAM invariante.

El PRAM invariante no garantiza que las tabulaciones cruzadas de las variables (a diferencia de las tabulaciones univariantes) permanezcan iguales.

# Ejecutamos nuevamente las variables clave

selectedKeyVarsHH <- c("URBRUR", "REGION", "HHSIZE", "OWNAGLAND", "RELIG")


HHVars <- c("IDH", selectedKeyVarsHH, pramVarsHH, numVarsHH, weightVarHH, strata_var) #agrega strata
fileHH <- file
fileHH <- fileHH[which(!duplicated(fileHH$IDH)),]
sdcHH <- createSdcObj(dat=fileHH, keyVars=selectedKeyVarsHH, pramVars=pramVarsHH, weightVar=weightVarHH, numVars = numVarsHH, strataVar = "strata_region")

sdcInitial <- sdcHH
sdc_respaldo <- sdcHH

En el Bloque 8.12, damos un ejemplo de PRAM invariante utilizando sdcMicro²⁵. PRAM es un método probabilístico y los resultados pueden diferir cada vez que aplicamos PRAM a las mismas variables de un conjunto de datos. Para superar esto y hacer que los resultados sean reproducibles, es una buena práctica establecer una semilla para el generador de números aleatorios en R, de modo que se generen los mismos números aleatorios cada vez²⁶. También, se muestra el número de registros modificados por variable.

8.3.1.1

Bloque 8.12 Producción de resultados reproducibles de PRAM utilizando set.seed()

# establecer la semilla para la generación de números aleatorios
set.seed(123) 
sdcInitial_edit <- pram(obj = sdcInitial)

sdcInitial_edit@pram$summary

##        variable nrChanges percChanges
## 1          ROOF        81        4.05
## 2        TOILET       247       12.35
## 3         WATER       177        8.85
## 4      ELECTCON         7        0.35
## 5      FUELCOOK       160        8.00
## 6 OWNMOTORCYCLE        62        3.10
## 7           CAR        19        0.95
## 8            TV       106        5.30
## 9     LIVESTOCK        23        1.15

La Tabla 8.9 muestra la tabulación de la variable después de aplicar el PRAM invariante. Podemos ver que las desviaciones de las tabulaciones iniciales, que tienen expectativa 0, son menores que la matriz de transición que no cumple la propiedad de invariancia. Las desviaciones restantes se deben a la aleatoriedad.

Tabla 8.9: Tabulación de la variable “región” antes y después del PRAM (invariante)

Valor	Tabulación antes de PRAM	Tabulación después de PRAM	Tabulación después del PRAM invariante
capital	5,000	5,052	4,998
rural1	500	457	499
rural2	400	391	403

La Tabla 8.10 presenta las tabulaciones cruzadas con la variable sexo. Antes de aplicar PRAM invariante, la proporción de hombres en la ciudad es mucho mayor que la de mujeres (alrededor del 60%). Esta propiedad no se mantiene después de PRAM invariante (los porcentajes de hombres y mujeres en la ciudad son aproximadamente iguales), aunque se mantienen las tabulaciones univariantes. Una solución es aplicar PRAM por separado para los hombres y las mujeres de este ejemplo²⁷. Esto puede hacerse especificando el argumento de los estratos en la función pram() de sdcMicro (véase más adelante).

Tabla 8.10: Tabulación cruzada de la variable “región” y la variable “sexo” antes y después del PRAM invariante

	Tabulación antes de PRAM		Tabulación después del PRAM invariante
Valor	hombre	mujer	hombre	mujer
capital	3,056	1,944	2,623	2,375
rural1	157	343	225	274
rural2	113	287	187	216

La función pram() en sdcMicro tiene varias opciones relacionadas a estratificación (strata_variables), entradas diagonales mínimas para utilizar una matriz de transición P personalizada (pd) y la cantidad de perturbación para el método Pram invariante, entregada mediante un vector numérico de longitud 1 (que se reciclará si es necesario) o un vector de la misma longitud que el número de variables.

Nota: Si no se establece ninguna opción y el método PRAM se aplica a un objeto sdcMicro, todas las variables PRAM seleccionadas en el objeto sdcMicro se utilizan automáticamente para PRAM y esta se aplica dentro de los estratos seleccionados (véase la sección Objetos de la clase sdcMicroObj sobre los objetos sdcMicro para más detalles).

8.3.1.2

Bloque 8.13 Selección de variables para aplicar PRAM

set.seed(123) # establecer la semilla para la generación de números aleatorios
# Aplicar PRAM solo a la variable TOILET
sdcInitial <- pram(obj = sdcInitial, variables = c ("TOILET"))
sdcInitial@pram$summary

##   variable nrChanges percChanges
## 1   TOILET       106         5.3

Los resultados de PRAM difieren si se aplican simultáneamente a varias variables o posteriormente a cada variable por separado. No es posible especificar toda la matriz de transición en sdcMicro, pero podemos establecer valores mínimos (entre 0 y 1) para las entradas diagonales. Las entradas diagonales especifican la probabilidad de que un determinado valor permanezca igual después de aplicar PRAM. Si fijamos el valor mínimo en 1, no habrá cambios en esta categoría. Por defecto, este valor es 0,8, que se aplica a todas las categorías. También es posible especificar un vector con valor para cada elemento diagonal de la transformación matriz/categoría. En el Bloque 8.14 los valores de la primera región tienen menos probabilidades de cambiar que los valores de las otras regiones.

Nota: El método PRAM invariante requiere que la matriz de transición tenga un valor propio unitario.

Por lo tanto, no se pueden utilizar todos los conjuntos de restricciones (por ejemplo, el valor mínimo 1 en cualquiera de las categorías).

8.3.1.3

Bloque 8.14 Especificación de los valores mínimos de la diagonal de la matriz de transición PRAM

sdcInitial <- sdc_respaldo # reasignar

sdcInitial <- pram(obj = sdcInitial, variables = c("TOILET"), pd = c(0.9)) #un valor por variable

sdcInitial@pram$summary

##   variable nrChanges percChanges
## 1   TOILET       133        6.65

En el método PRAM invariante, también podemos especificar la cantidad de perturbaciones especificando el parámetro alfa. Esta elección se refleja en la matriz de transición. Por defecto, el valor de alfa es 0,5. Cuanto mayor sea alfa, mayores serán las perturbaciones. Un valor de alfa igual a cero no produce cambios. El valor máximo de alfa es 1.

PRAM es especialmente útil cuando un conjunto de datos contiene muchas variables y la aplicación de otros métodos de anonimización, como la recodificación y la supresión local, conduciría a una pérdida significativa de información. Las comprobaciones del riesgo y la utilidad son importantes después de PRAM.

Para hacer inferencia estadística sobre las variables a las que se aplicó PRAM, el investigador necesita conocer el método PRAM, así como la matriz de transición. Sin embargo, la matriz de transición, junto con la semilla de números aleatorios, puede conducir a la divulgación mediante la reconstrucción de los valores no perturbados. Por lo tanto, se recomienda publicar la matriz de transición, pero nunca la semilla aleatoria.

Una desventaja del uso de PRAM es que se pueden generar combinaciones muy improbables, como la de una persona de 63 años que va a la escuela. Por lo tanto, es necesario auditar las variables PRAM para evitar que tales combinaciones se produzcan en el archivo de datos publicado. En principio, la matriz de transición puede diseñarse de forma que ciertas transiciones no sean posibles (probabilidad 0). Por ejemplo, para los que van a la escuela, la edad debe oscilar entre los 6 y los 18 años y solo se permiten esos cambios. En sdcMicro la matriz de transición no puede especificarse exactamente. Una alternativa útil es construir estratos y aplicar PRAM dentro de los estratos. De este modo, los cambios entre variables solo se aplicarán dentro de los estratos. El Bloque 8.15 ilustra esto aplicando PRAM a la variable “toilet” dentro de los estratos generados por la “region”. Esto evita que se produzcan cambios en la variable “toilet”, donde se intercambian los tipos de inodoros de una determinada región con los de otras regiones. Por ejemplo, en la región de la capital no se utilizan ciertos tipos de inodoros no mejorados y, por lo tanto, estas combinaciones no deberían producirse después de aplicar PRAM. Los valores solo se cambian con los que están disponibles en el mismo estrato. Los estratos pueden estar formados por cualquier variable categórica, por ejemplo, sexo, grupos de edad, nivel de educación.

8.3.1.4

Bloque 8.15 Minimizar las combinaciones improbables aplicando el PRAM por estratos

sdcInitial <- sdc_respaldo # reasignar

#Aplicar PRAM dentro de los estratos formados por la variable educ
sdcInitial <- pram(obj = sdcInitial, variables = c("TOILET"), strata_variables = c("REGION"))

sdcInitial@pram$summary

##   variable nrChanges percChanges
## 1   TOILET       158         7.9

Lectura recomendada de PRAM:
- Gouweleeuw, J. M, P Kooiman, L.C.R.J Willenborg, and P.P de Wolf. “Post Randomization for Statistical Disclosure Control: Theory and Implementation.” Journal of Official Statistics 14, no. 4 (1998a): 463-478. Available at http://www.jos.nu/articles/abstract.asp?article=144463
- Gouweleeuw, J. M, P Kooiman, L.C.R.J Willenborg, and Peter Paul de Wolf. “The Post Randomization Method for Protecting Microdata.” Qüestiió, Quaderns d’Estadística i Investigació Operativa 22, no. 1 (1998b): 145-156. Available at http://www.raco.cat/index.php/Questiio/issue/view/2250
- Marés, Jordi, and Vicenç Torra. 2010.”PRAM Optimization Using an Evolutionary Algorithm.” In Privacy in Statistical Databases, by Josep Domingo-Ferrer and Emmanouil Magkos, 97-106. Corfú, Greece: Springer.
- Warner, S.L. “Randomized Response: A Survey Technique for Eliminating Evasive Answer Bias.” Journal of American Statistical Association 57 (1965): 622-627.

8.3.2 Microagregación

La microagregación es más adecuada para las variables continuas, pero puede extenderse en algunos casos a las variables categóricas²⁸. Es más útil cuando se han predeterminado reglas de confidencialidad (por ejemplo, se ha establecido un determinado umbral de \(k\)-anonimato) que permiten la divulgación de datos solo si las combinaciones de variables son compartidas por más de un número umbral predeterminado de encuestados (\(k\)). El primer paso en la microagregación es la formación de pequeños grupos de individuos que sean homogéneos con respecto a los valores de las variables seleccionadas, como grupos con ingresos o edad similares. Posteriormente, los valores de las variables seleccionadas de todos los miembros del grupo se sustituyen por un valor común, por ejemplo, la media de ese grupo. Los métodos de microagregación difieren en cuanto a (i) cómo se define la homogeneidad de los grupos, (ii) los algoritmos utilizados para encontrar grupos homogéneos y (iii) la determinación de los valores de sustitución. En la práctica, la microagregación funciona mejor cuando los valores de las variables de los grupos son más homogéneos. En ese caso, la pérdida de información debida a la sustitución de valores por valores comunes para el grupo será menor que en los casos en que los grupos son menos homogéneos.

En el caso univariante, y también para las variables categóricas ordinales, la formación de grupos homogéneos es sencilla: los grupos se forman ordenando primero los valores de la variable y luego creando \(g\) grupos de tamaño \(n_i\) para todos los grupos \(i\) en \(1, ..., g\). Esto maximiza la homogeneidad dentro del grupo, que se mide por la suma al cuadrado de los residuos dentro de los grupos (\(SSE\))

\[ SSE = \sum_{i = 1}^{g}{\sum_{j = 1}^{n_{i}}{\left( x_{ij} - {\overline{x}}_{i} \right)^{T}\left( x_{ij} - {\overline{x}}_{i} \right)}} \]

Cuanto menor sea \(SSE\), mayor será la homogeneidad dentro del grupo. El tamaño de los grupos puede variar entre ellos, pero a menudo se utilizan grupos de igual tamaño para simplificar la búsqueda²⁹.

La función microaggregation() de sdcMicro puede utilizarse para la microagregación univariante. El argumento “aggr” especifica el tamaño del grupo. La formación de grupos es más fácil si todos los grupos -excepto quizá el último grupo de los restantes- tienen el mismo tamaño. Este es el caso en la implementación en sdcMicro, ya que no es posible tener grupos de diferentes tamaños. El Bloque 8.16 muestra cómo utilizar la función microaggregation() en sdcMicro³⁰. El tamaño de grupo por defecto es 3, pero el usuario puede especificar cualquier tamaño de grupo deseado. La elección del tamaño del grupo depende de la homogeneidad dentro de los grupos y del nivel de protección requerido. En general, cuanto más grande sea el grupo, mayor será la protección. Una desventaja de los grupos de igual tamaño es que los datos pueden ser inadecuados para ello. Por ejemplo, si dos individuos tienen un ingreso bajo (por ejemplo, 832 y 966) y cuatro individuos tienen un ingreso alto (por ejemplo, 3.313, 3.211, 2.987, 3.088), la media de dos grupos de tamaño tres (por ejemplo, (832 + 966 + 2.987) / 3 = 1.595 y (3.088 + 3.211 + 3.313) / 3 = 3.204) no representaría ni el ingreso bajo ni el alto.

8.3.2.1

Bloque 8.16 Aplicación de la microagregación con la función sdcMicro microaggregation()

sdcInitial <- sdc_respaldo # reasignar

sdcInitial <- microaggregation(obj = sdcInitial, variables = "INCTOTGROSSHH", aggr = 3, method = "mdav", measure = "mean")

Por defecto, la función de microagregación sustituye los valores por la media del grupo. Un enfoque alternativo y más robusto es reemplazar los valores del grupo con la mediana. Esto puede especificarse en el argumento “measure” de la función microaggregation(). En los casos en que se elige la mediana, un individuo de cada grupo mantiene el mismo valor si los grupos tienen tamaños impares. En los casos en los que hay un alto grado de heterogeneidad dentro de los grupos (suele ser el caso de los grupos más grandes), se prefiere la mediana para preservar la información de los datos. Un ejemplo es el ingreso, donde un valor atípico puede dar lugar a múltiples valores atípicos cuando se utiliza la microagregación. Esto se ilustra en la Tabla 8.11. Si elegimos la media como reemplazo de todos los valores, que se agrupan con el valor atípico (6,045 en el grupo 2), a estos registros se les asignarán valores alejados de sus valores originales. Si elegimos la mediana, los ingresos de los individuos 1 y 2 no se ven alterados, pero ningún valor es un valor atípico. Por supuesto, esto puede plantear problemas en sí mismo. En el caso de que la microagregación se aplique a variables categóricas, se utiliza la mediana (el valor en el grupo que más se repite) para calcular el valor de reemplazo de aquel grupo.

Nota: Si la microagregación altera los valores atípicos, esto puede tener un impacto significativo en el cálculo de algunas medidas sensibles a los valores atípicos, como el índice GINI.

Tabla 8.11: Ilustración del efecto de la elección de la media frente a la mediana para la microagregación cuando se trata de valores atípicos

ID	Grupo	Ingresos	Microagregación (media)	Microagregación (mediana)
1	1	2,300	2,245	2,300
2	2	2,434	3,608	2,434
3	1	2,123	2,245	2,300
4	1	2,312	2,245	2,300
5	2	6,045	3,608	2,434
6	2	2,345	3,608	2,434

En el caso de múltiples variables candidatas a la microagregación, una posibilidad es aplicar la microagregación univariante a cada una de las variables por separado. La ventaja de la microagregación univariante es la mínima pérdida de información, ya que los cambios en las variables son limitados. Sin embargo, la literatura muestra que el riesgo de divulgación puede ser muy alto si la microagregación univariante se aplica a varias variables por separado y no se aplican técnicas adicionales de anonimización (Josep Domingo-Ferrer et al. 2002). Para superar este inconveniente, una alternativa a la microagregación univariante es la microagregación multivariante.

La microagregación multivariada se utiliza ampliamente en las estadísticas oficiales (Benschop, Machingauta, and Welch 2019). El primer paso de la agregación multivariante es la creación de grupos homogéneos basados en varias variables. Los grupos se forman a partir de las distancias multivariadas entre los individuos. Posteriormente, los valores de todas las variables para todos los miembros del grupo se sustituyen por los mismos valores. La Tabla 8.12 lo ilustra con tres variables. Vemos que la agrupación por ingresos, gastos y patrimonio conduce a una agrupación diferente, como en el caso de la Tabla 8.11, en la que los grupos se formaron basándose solo en los ingresos.

Tabla 8.12: Ilustración de la microagregación multivariante

		Antes de microagregación			Después de microagregación
ID	Grupo	Ingreso	Gasto	Patrimonio	Ingreso	Gasto	Patrimonio
1	1	2,300	1,714	5.3	2,285.7	1,846.3	6.3
2	1	2,434	1,947	7.4	2,285.7	1,846.3	6.3
3	1	2,123	1,878	6.3	2,285.7	1,846.3	6.3
4	2	2,312	1,950	8.0	3,567.3	2,814.0	8.3
5	2	6,045	4,569	9.2	3,567.3	2,814.0	8.3
6	2	2,345	1,923	7.8	3,567.3	2,814.0	8.3

Existen varios métodos de microagregación multivariante que difieren en cuanto al algoritmo utilizado para crear grupos de individuos. Además, existe un trade-off entre la velocidad del algoritmo y la homogeneidad dentro del grupo, que está directamente relacionada con la pérdida de información. En el caso de los grandes conjuntos de datos, esto es especialmente difícil. En este artículo se analiza con más detalle el algoritmo de distancia máxima al vector medio (MDAV). El algoritmo MDAV fue introducido por primera vez por (Josep Domingo-Ferrer and Torra 2005) y representa una buena opción con respecto a la compensación entre el tiempo de cálculo y la homogeneidad del grupo, calculada por el \(SSE\) dentro del grupo. El algoritmo MDAV está implementado en sdcMicro.

El algoritmo calcula un registro medio o centroide \(C\), que contiene los valores medios de todas las variables incluidas. Seleccionamos un individuo \(A\) con la mayor distancia euclidiana al cuadrado respecto a \(C\), y construimos un grupo de \(k\) registros alrededor de \(A\). El grupo de \(k\) registros está formado por \(A\) y los \(k-1\) registros más cercanos a \(A\) medidos por la distancia euclidiana. A continuación, seleccionamos otro individuo \(B\), con la mayor distancia euclidiana al cuadrado desde el individuo \(A\). Con los registros restantes, construimos un grupo de \(k\) registros alrededor de \(B\). De la misma manera, seleccionamos un individuo \(D\) con la mayor distancia desde \(B\) y, con los registros restantes, construimos un nuevo grupo de \(k\) registros alrededor de \(D\). El proceso se repite hasta que nos queden menos de \(2∗k\) registros. El algoritmo MDAV crea grupos de igual tamaño con la excepción, quizá, de un último grupo con los remanentes. El conjunto de datos microagregados se calcula sustituyendo cada registro del conjunto de datos original por los valores medios del grupo al que pertenece. Sin embargo, los tamaños de grupo iguales pueden no ser ideales para los datos caracterizados por tener una alta variabilidad. En sdcMicro la microagregación multivariante también se implementa en la función microaggregation(). El Bloque 8.17 muestra cómo elegir el algoritmo MDAV en sdcMicro.

8.3.2.2

Bloque 8.17 Microagregación multivariada con el algoritmo de distancia máxima al vector medio (MDAV) en sdcMicro

sdcInitial <- createSdcObj(dat=fileHH, keyVars=selectedKeyVarsHH, pramVars=pramVarsHH, weightVar=weightVarHH, numVars = numVarsHH) # reasignar sin strata var

sdcInitial <- microaggregation(obj = sdcInitial, variables = c("INCTOTGROSSHH", "TANHHEXP"), method = "mdav")

#sdc_respaldo@origData %>% view()

También es posible agrupar las variables solo dentro de los estratos. Esto reduce el tiempo de cálculo y añade una capa adicional de protección a los datos, debido a la mayor incertidumbre producida ³¹. En sdcMicro esto puede lograrse especificando las variables de estrato, como se muestra en el Bloque 8.18.

8.3.2.3

Bloque 8.18 Especificación de variables de estrato para la microagregación

sdcInitial <- sdc_respaldo # reasignar con variable de estrato incluida

sdcInitial <- microaggregation(obj = sdcInitial, variables = c("INCTOTGROSSHH", "TANHHEXP"), method = "mdav")#

# No corre el estrato en opción: strata_variables = c("strata_region")

Además del método MDAV, hay algunos otros métodos de agrupación implementados en sdcMicro (Matthias Templ Bernhard Meindl and Kowarik 2014). La Tabla 8.13 ofrece un resumen de estos métodos. Mientras que el método “MDAV” utiliza la distancia euclidiana, el método “rmd” utiliza la distancia de Mahalanobis. Una alternativa a estos métodos es la clasificación de los encuestados basada en el primer componente principal (CP), que es la proyección de todas las variables en un espacio unidimensional que maximiza la varianza de esta proyección. El rendimiento de este método depende de la parte de la varianza total de los datos que explica el primer CP. El método “rmd” es más intensivo desde el punto de vista computacional debido al cálculo de las distancias de Mahalanobis, pero proporciona mejores resultados con respecto a la homogeneidad de los grupos. Se recomienda para conjuntos de datos más pequeños (Matthias Templ Bernhard Meindl and Kowarik 2014).

Tabla 8.13: Métodos de agrupación para la microagregación que son implementados en sdcMicro

Método / opción en sdcMicro	Descripción
mdav	la agrupación se basa en medidas de distancia clásicas (euclidianas)
rmd	la agrupación se basa en medidas de distancia multivariante robusta (Mahalanobis)
pca	la agrupación se basa en el análisis de componentes principales, mientras que los datos se clasifican según el primer componente principal
clustpppca	la agrupación se basa en el clustering y en el análisis de componentes principales (robusto) para cada cluster
influence	la agrupación se basa en el clustering y la agregación se realiza dentro de los clusters

En el caso de que se utilicen múltiples variables para la microagregación, se recomienda examinar primero la matriz de covarianza o de correlación de estas variables. Si no todas las variables están bien correlacionadas, pero dos o más conjuntos de variables muestran una alta correlación, se producirá una menor pérdida de información al aplicar la microagregación por separado a estos conjuntos de variables. En general, si las variables están muy correlacionadas, se producirá una menor pérdida de información al aplicar la microagregación multivariante. La ventaja de sustituir los valores por la media de los grupos en lugar de otros valores de sustitución tiene la ventaja de que se conservan las medias globales de las variables.

Lectura recomendada de microagregación:
- Domingo-Ferrer, Josep, and Josep Maria Mateo-Sanz. 2002.”Practical data-oriented microaggregation for statistical disclosure control.” IEEE Transactions on Knowledge and Data Engineering 14 (2002): 189-201.
- Hansen, Stephen Lee, and Sumitra Mukherjee. 2003. “A polynomial algorithm for univariate optimal.” IEEE Transactions on Knowledge and Data Engineering 15 (2003): 1043-1044.
- Hundepool, Anco, Josep Domingo-Ferrer, Luisa Franconi, Sarah Giessing, Rainer Lenz, Jane Naylor, Eric Schulte Nordholt, Giovanni Seri, and Peter Paul de Wolf. 2006. Handbook on Statistical Disclosure Control. ESSNet SDC. http://neon.vb.cbs.nl/casc/handbook.htm
- Hundepool, Anco, Josep Domingo-Ferrer, Luisa Franconi, Sarah Giessing, Eric Schulte Nordholt, Keith Spicer, and Peter Paul de Wolf. 2012. Statistical Disclosure Control. Chichester: John Wiley & Sons Ltd. doi:10.1002/9781118348239.
- Templ, Matthias, Bernhard Meindl, Alexander Kowarik, and Shuang Chen. 2014, August. “International Household Survey Network (IHSN).” http://www.ihsn.org/home/software/disclosure-control-toolbox. (accessed July 9, 2018).

8.3.3 Adición de ruido

La adición de ruido o enmascaramiento, consiste en añadir o restar valores (pequeños) a los valores originales de una variable, y es lo más adecuado para proteger las variables continuas (véase (Brand 2002) para una visión general). La adición de ruido puede impedir la coincidencia exacta de las variables continuas. Las ventajas de la adición de ruido son que el ruido es típicamente continuo con media cero, y la coincidencia exacta con archivos externos no será posible. Sin embargo, dependiendo de la magnitud del ruido añadido, la comparación aproximada de intervalos puede ser posible.

Cuando se utiliza la adición de ruido para proteger los datos, es importante tener en cuenta el tipo de datos, el uso previsto de los mismos y las propiedades de los datos antes y después de la adición de ruido, es decir, la distribución -en particular la media-, la covarianza y la correlación entre los conjuntos de datos perturbados y los originales.

Dependiendo de los datos, también puede ser útil comprobar que los valores perturbados están dentro de un rango de valores con sentido. La 8.9 ilustra los cambios en la distribución de los datos con niveles crecientes de ruido. En el caso de los datos que tienen valores atípicos, es importante señalar que cuando la distribución de los datos perturbados es similar a la distribución de los datos originales (por ejemplo, con niveles de ruido bajos), la adición de ruido no protegerá los valores atípicos. Después de la adición de ruido, estos valores atípicos generalmente pueden seguir detectándose como tales y, por tanto, identificarse fácilmente. Un ejemplo es un único valor de ingreso muy elevado en una determinada región. Después de perturbar este valor de ingreso, el valor seguirá siendo reconocido como el ingreso más alto de esa región y, por tanto, puede utilizarse para la reidentificación. Esto se ilustra en la 8.8, donde se representan 10 observaciones originales (círculos abiertos) y las observaciones anonimizadas (triángulos rojos). La décima observación es un valor atípico. Los valores de las nueve primeras observaciones están suficientemente protegidos por la adición de ruido: su magnitud y orden han cambiado y se puede evitar con éxito la coincidencia exacta o por intervalos. El valor atípico no está suficientemente protegido, ya que, tras la adición de ruido, el valor atípico puede seguir identificándose fácilmente. El hecho de que el valor absoluto haya cambiado no es una protección suficiente. Por otro lado, con niveles de ruido elevados, la protección es mayor incluso para los valores atípicos, pero la estructura de los datos no se conserva y la pérdida de información es grande, lo que no es una situación ideal. Una forma de sortear el problema de los valores atípicos es añadir ruido de mayor magnitud a los valores atípicos que a los demás valores.

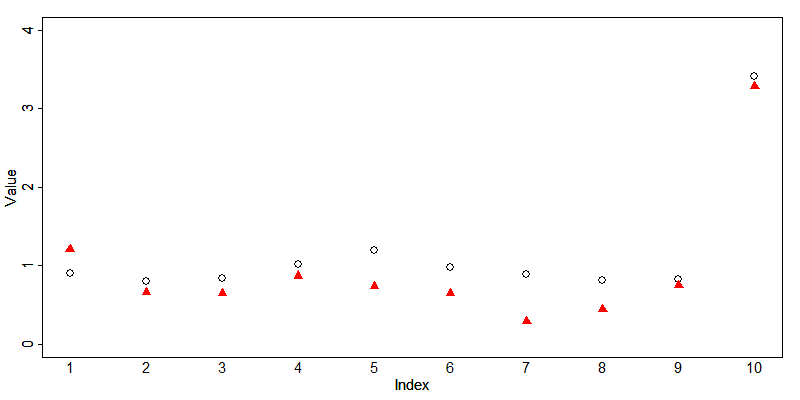
Figura 8.8: Ilustración del efecto de la adición de ruido a los valores atípicos

Existen varios algoritmos de adición de ruido. La versión más simple de la adición de ruido es el ruido aditivo no correlacionado normalmente distribuido, donde \(x_j\), los valores originales de la variable \(j\) son reemplazados por

\[z_{j} = x_{j} + \varepsilon_{j},\]

donde \(\varepsilon_{j} \sim N(0, \sigma_{\varepsilon_{j}}^{2})\) y \(\sigma_{\varepsilon_{j}} = \alpha * \sigma_{j}\) con \(\sigma_{j}\) la desviación estándar de los datos originales. De este modo, se conservan la media y las covarianzas, pero no las varianzas ni el coeficiente de correlación. Si el nivel de ruido añadido \(\alpha\), se da a conocer al usuario, se pueden estimar muchos estadísticos de forma coherente a partir de los datos perturbados. El ruido añadido es proporcional a la varianza de la variable original. La magnitud del ruido añadido se especifica mediante el parámetro α, que especifica esta proporción. La desviación estándar de los datos perturbados es \(1 + \alpha\) veces la desviación estándar de los datos perturbados. La decisión sobre la magnitud del ruido añadido debe estar informada por la situación legal relativa a la privacidad de los datos, la sensibilidad de los datos y los niveles aceptables de riesgo de divulgación y pérdida de información. En general, el nivel de ruido es una función de la varianza de las variables originales, el nivel de protección necesario y el rango de valores deseado tras la anonimización³². Un valor \(\alpha\) demasiado pequeño dará lugar a una protección insuficiente, mientras que un valor \(\alpha\) demasiado alto hará que los datos sean inútiles para los usuarios.

En sdcMicro la adición de ruido se implementa en la función addNoise(). El algoritmo y el parámetro pueden especificarse como argumentos en la función addNoise(). La adición de ruido simple se implementa en la función addNoise() con el valor “additive” para el argumento “method”. El Bloque 8.19 muestra cómo utilizar sdcMicro para añadir ruido no correlacionado a las variables de gasto, donde la desviación estándar del ruido añadido es igual a la mitad de la desviación estándar de las variables originales³³. El ruido se añade a todas las variables seleccionadas.

8.3.3.1

Bloque 8.19 Adición de ruido no correlacionado

sdcInitial <- addNoise(obj = sdcInitial, variables = c("TFOODEXP", "TALCHEXP", "TCLTHEXP", "THOUSEXP", 
                                                       "TFURNEXP", "THLTHEXP", "TTRANSEXP", "TCOMMEXP",
                                                       "TRECEXP", "TEDUEXP", "TRESTHOTEXP", "TMISCEXP"), 
                       noise = 0.5, method = "additive")

La 8.9 muestra la distribución de frecuencias de una variable numérica continua y la distribución antes y después de la adición de ruido con diferentes niveles de ruido (0.1, 0.5, 1, 2 y 5). El primer gráfico muestra la distribución de los valores originales. Los histogramas muestran claramente que el ruido de grandes magnitudes (valores altos de alfa) conduce a una distribución de los datos alejada de los valores originales. La distribución de los datos pasa a ser una distribución normal cuando la magnitud del ruido crece respectivamente a la varianza de los datos. La media de los datos se conserva, pero, al aumentar el nivel de ruido, la varianza de los datos perturbados crece. Tras añadir un ruido de magnitud 5, la distribución de los datos originales queda completamente alterada.

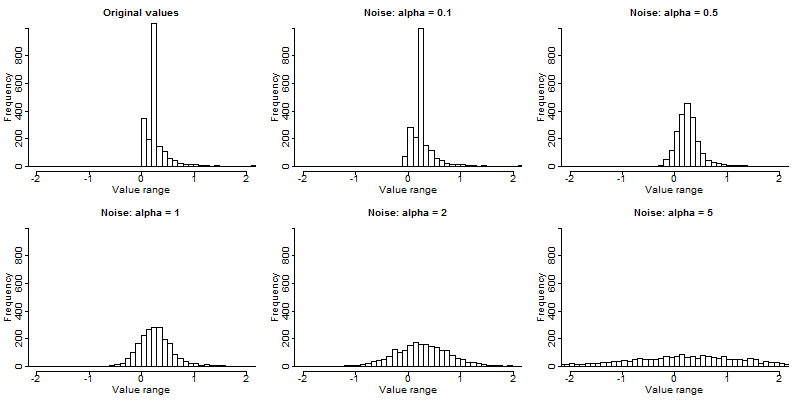
Figura 8.9: Distribución de frecuencias de una variable continua antes y después de la adición de ruido

La 8.10 muestra el rango de valores de una variable antes de añadir ruido (sin ruido) y después de añadir varios niveles de ruido (α de 0,1 a 1,5 con incrementos de 0,1). En la figura se representan el valor mínimo, los percentiles 20, 30 y 40, la mediana, los percentiles 60, 70, 80 y 90 y el valor máximo. La mediana (percentil 50) se indica con el símbolo rojo “\(\color {red}{\text{+}}\)”. De las 8.9 y 8.10 se desprende que el rango de valores se amplía tras la adición de ruido, y que la mediana se mantiene aproximadamente en el mismo nivel, al igual que la media por construcción. Cuanto mayor sea la magnitud del ruido añadido, mayor será el rango de valores. En los casos en que la variable debe permanecer en un determinado rango de valores (por ejemplo, solo valores positivos, entre 0 y 100), esto puede ser una desventaja de la adición de ruido. Por ejemplo, las variables de gasto suelen tener valores no negativos, pero la adición de ruido a estas variables puede generar valores negativos, que son difíciles de interpretar. Una forma de evitar este problema es poner a cero los valores negativos. Sin embargo, este truncamiento de los valores por debajo de un determinado umbral distorsionará la distribución (matriz de media y varianza) de los datos perturbados. Esto significa que las características que se preservaron con la adición de ruido, como la conservación de la media y la matriz de covarianza, se pierden y el usuario, incluso con el conocimiento de la magnitud del ruido, ya no puede utilizar los datos para una estimación coherente.

Otra forma de evitar los valores negativos es la aplicación de ruido multiplicativo en lugar de aditivo. En ese caso, las variables se multiplican por un factor aleatorio con esperanza 1 y varianza positiva. Esto también dará lugar a mayores perturbaciones (en valor absoluto) de los valores atípicos. Si la varianza del ruido añadido es pequeña, no habrá factores negativos o serán pocos y, por tanto, habrá menos cambios de signo que en el caso del enmascaramiento por ruido aditivo. El enmascaramiento de ruido multiplicativo no está implementado en sdcMicro, pero puede implementarse con relativa facilidad en R base generando un vector de números aleatorios y multiplicando los datos con este vector. Para más información sobre el enmascaramiento de ruido multiplicativo y las propiedades de los datos después del enmascaramiento, nos remitimos a (Kim and Winkler 2003).

Figura 8.10: Niveles de ruido y el impacto en el rango de valores (percentiles)

Si se seleccionan dos o más variables para la adición de ruido, se prefiere la adición de ruido correlacionado para preservar la estructura de correlación en los datos. En este caso, la matriz de covarianza del ruido \(\Sigma_{\varepsilon}\) es proporcional a la matriz de covarianza de los datos originales \(\Sigma_{X}\):

\[\Sigma_{\varepsilon} = \alpha \Sigma_{X}\]

En la función addNoise() del paquete sdcMicro, se puede utilizar la adición de ruido correlacionado especificando los métodos “correlated” o “correlated2”. El método “correlated” asume que las variables se distribuyen aproximadamente de forma normal. El método “correlated2” es una versión del método “correlated”, que es robusto contra el supuesto de normalidad. El Bloque 8.20 muestra cómo utilizar el método “correlated2”. La normalidad de las variables puede investigarse en R, con, por ejemplo, un test Jarque-Bera o Shapiro-Wilk³⁴.

8.3.3.2

Bloque 8.20 Adición de ruido correlacionado

sdcInitial <- addNoise(obj = sdcInitial, variables = c("TFOODEXP", "TALCHEXP", "TCLTHEXP", "THOUSEXP", 
                                                       "TFURNEXP", "THLTHEXP", "TTRANSEXP", "TCOMMEXP", 
                                                       "TRECEXP", "TEDUEXP", "TRESTHOTEXP", "TMISCEXP"), 
                       noise = 0.5, method = "correlated2")

En muchos casos, solo hay que proteger los valores atípicos, o hay que protegerlos más. El método “outdect” añade ruido solo a los valores atípicos, lo que se ilustra en el Bloque 8.21. Los valores atípicos se identifican con métodos univariantes y multivariantes robustos basados en una distancia de Mahalanobis robusta calculada por el estimador MCD (A. K. Matthias Templ Bernhard Meindl and Chen 2014). Sin embargo, la adición de ruido no es el método más adecuado para la protección de los valores atípicos.

8.3.3.3

Bloque 8.21 Adición de ruido para los valores atípicos mediante el método “outdect”

sdcInitial <- addNoise(obj = sdcInitial, variables = c("TFOODEXP", "TALCHEXP", "TCLTHEXP", "THOUSEXP", 
                                                       "TFURNEXP", "THLTHEXP", "TTRANSEXP", "TCOMMEXP", 
                                                       "TRECEXP", "TEDUEXP", "TRESTHOTEXP", "TMISCEXP"), 
                       noise = 0.5, method = "outdect")

Si la adición de ruido se aplica a variables que son una proporción de un agregado, esta estructura puede verse seriamente alterada por la adición de ruido. Los ejemplos son los datos de ingresos y gastos con muchas categorías de ingresos y gastos. Las categorías suman el total de ingresos o el total de gastos. En los datos originales, los agregados coinciden con la suma de los componentes. Sin embargo, después de añadir ruido a sus componentes (por ejemplo, diferentes categorías de gasto), sus nuevos agregados ya no coincidirán necesariamente con la suma de las categorías. Una forma de mantener esta estructura es añadir ruido solo a los agregados y liberar los componentes como relación de los agregados perturbados. El Bloque 8.22 ilustra esto añadiendo ruido al total de los gastos. Posteriormente, se utilizan los cocientes de las categorías de gasto iniciales para cada individuo para reconstruir los valores perturbados de cada categoría de gasto.

8.3.3.4

Bloque 8.22 Adición de ruido a agregados y sus componentes

# añadir ruido a los totales (ingresos / gastos)
sdcInital <- addNoise(noise = 0.5, obj = sdcInitial, variables=c("TANHHEXP", "INCTOTGROSSHH"), method="additive") 

# multiplicar los totales anonimizados por los ratios para obtener los componentes anonimizados
compExp <-  c("TFOODEXP", "TALCHEXP", "TCLTHEXP", "THOUSEXP", 
              "TFURNEXP", "THLTHEXP", "TTRANSEXP", "TCOMMEXP", 
              "TRECEXP", "TEDUEXP", "TRESTHOTEXP", "TMISCEXP")

sdcInital@manipNumVars[,compExp] <- sdcInital @manipNumVars[,"TANHHEXP"] * 
                                      sdcInital @origData[,compExp]/ sdcInital@origData[,"TANHHEXP"]

# recalcular los riesgos después de cambiar manualmente los valores en el objeto sdcMicro
calcRisks(sdcInital)

## The input dataset consists of 2000 rows and 40 variables.
##   --> Categorical key variables: URBRUR, REGION, HHSIZE, OWNAGLAND, RELIG
##   --> Numerical key variables: LANDSIZEHA, TANHHEXP, TFOODEXP, TALCHEXP, TCLTHEXP, THOUSEXP, TFURNEXP, THLTHEXP, TTRANSEXP, TCOMMEXP, TRECEXP, TEDUEXP, TRESTHOTEXP, TMISCEXP, INCTOTGROSSHH, INCRMT, INCWAGE, INCFARMBSN, INCNFARMBSN, INCRENT, INCFIN, INCPENSN, INCOTHER
##   --> Weight variable: WGTPOP
##   --> Strata variable(s): strata_region
## ----------------------------------------------------------------------

## Information on categorical key variables:
## 
## Reported is the number, mean size and size of the smallest category >0 for recoded variables.
## In parenthesis, the same statistics are shown for the unmodified data.
## Note: NA (missings) are counted as seperate categories!

##  Key Variable Number of categories      Mean size            Size of smallest (>0)      
##        URBRUR                    2  (2)  1000.000 (1000.000)                   684 (684)
##        REGION                    6  (6)   333.333  (333.333)                   260 (260)
##        HHSIZE                   23 (23)    86.957   (86.957)                     1   (1)
##     OWNAGLAND                    4  (4)   531.667  (531.667)                   332 (332)
##         RELIG                    7  (7)   166.667  (166.667)                     7   (7)

## ----------------------------------------------------------------------

## Infos on 2/3-Anonymity:
## 
## Number of observations violating
##   - 2-anonymity: 115 (5.750%)
##   - 3-anonymity: 239 (11.950%)
##   - 5-anonymity: 497 (24.850%)
## 
## ----------------------------------------------------------------------

## Numerical key variables: LANDSIZEHA, TANHHEXP, TFOODEXP, TALCHEXP, TCLTHEXP, THOUSEXP, TFURNEXP, THLTHEXP, TTRANSEXP, TCOMMEXP, TRECEXP, TEDUEXP, TRESTHOTEXP, TMISCEXP, INCTOTGROSSHH, INCRMT, INCWAGE, INCFARMBSN, INCNFARMBSN, INCRENT, INCFIN, INCPENSN, INCOTHER
## 
## Disclosure risk is currently between [0.00%; 65.50%]
## 
## Current Information Loss:
##   - IL1: 5502068.37
##   - Difference of Eigenvalues: -3410140045704050.500%
## ----------------------------------------------------------------------

Lectura recomendada de adición de ruido:
- Brand, Ruth. 2002. “Microdata Protection through Noise Addition.” In Inference -Control in Statistical Databases - From Theory to Practice, edited byJosep Domingo-Ferrer. Lecture Notes in Computer Science Series 2316, 97-116. Berlin Heidelberg: Springer. http://link.springer.com/chapter/10.1007%2F3-540-47804-3_8
- Kim, Jay J, and William W Winkler. 2003. “Multiplicative Noise for Masking Continuous Data.” Research Report Series (Statistical Research Division. US Bureau of the Census). https://www.census.gov/srd/papers/pdf/rrs2003-01.pdf
- Torra, Vicenç, and Isaac Cano. 2011. “Edit Constraints on Microaggregation and Additive Noise.” In Privacy and Security Issues in Data Mining and Machine Learning, edited by C. Dimitrakakis, A. Gkoulalas-Divanis, A. Mitrokotsa, V. S. Verykios, Y. Saygin. Lecture Notes in Computer Science Volume 6549, 1-14. Berlin Heidelberg: Springer. http://link.springer.com/book/10.1007/978-3-642-19896-0
- Mivule, K. 2013. “Utilizing Noise Addition for Data Privacy, An Overview.” Proceedings of the International Conference on Information and Knowledge Engineering (IKE 2012), (pp.65-71).Las Vegas, USA. http://arxiv.org/ftp/arxiv/papers/1309/1309.3958.pdf

8.3.4 Rank swapping (Intercambio de rangos)

Rank swapping se basa en intercambiar los valores de una determinada variable entre los registros. Rank swapping es un tipo de intercambio de datos, que se define para las variables ordinales y continuas. Para Rank swapping, los valores de la variable se ordenan primero. El número posible de valores con los que se puede intercambiar una variable está limitado por los valores que se encuentran alrededor del valor original al ordenar los valores del conjunto de datos. El tamaño de este vecindario puede especificarse, por ejemplo, como un porcentaje del número total de observaciones. Esto también significa que un valor puede ser intercambiado con valores iguales o muy similares. Esto es especialmente cierto si la vecindad es pequeña o si solo hay unos pocos valores diferentes en la variable (variable ordinal). Un ejemplo es la variable “educación” si tiene pocas categorías: (“ninguna”, “primaria”, “secundaria”, “terciaria”). En estos casos, Rank swapping no es un método adecuado al encontrarse con pocas categorías y limitarse por los valores que se encuentran alrededor, para que fuese adecuado, tendría que contar con un número mayor de categorías a intercambiar.

Si Rank swapping se aplica a varias variables en simultáneo, la estructura de correlación entre las variables se mantiene. Por lo tanto, es importante comprobar si la estructura de correlación en los datos es plausible. Rank swapping se implementa en la función rankSwap() de sdcMicro. Las variables que deben intercambiarse deben especificarse en el argumento “variables”. Por defecto, los valores por debajo del percentil 5 y por encima del percentil 95 se codifican por arriba y por abajo y se sustituyen por su valor medio (véase la sección Codificación superior e inferior). Especificando las opciones “TopPercent” y “BottomPercent” podemos elegir estos percentiles. El argumento “p” define el tamaño de la vecindad como porcentaje del tamaño de la muestra. Si el valor “p” es 0.05, el vecindario tendrá un tamaño de \(0.05 * n\), donde \(n\) es el tamaño de la muestra. Dado que Rank swapping es un método probabilístico, es decir, el intercambio depende de un mecanismo generador de números aleatorios, se recomienda especificar una semilla para el generador de números aleatorios antes de utilizar Rank swapping y así garantizar la reproducibilidad de los resultados. La semilla también puede especificarse como argumento de la función rankSwap(). El Bloque 8.23 muestra cómo aplicar Rank swapping con sdcMicro. Si las variables contienen valores perdidos (NA en R), la función rankSwap() los recodificará automáticamente con el valor especificado en el argumento “missing”. Este valor no debe estar en el rango de valores de ninguna de las variables. Después de utilizar la función rankSwap(), estos valores deberían recodificarse como NA. Esto se muestra en el Bloque 8.23.

8.3.4.1

Bloque 8.23 Rank swapping usando sdcMicro

# establecer la semilla para el generador de números aleatorios 
set.seed(12345) 

# comprobar la estructura de correlación entre las variables
cor(file$THOUSEXP, file$TFOODEXP)

## [1] 0.3811335

# aplicar rank swapping
rankSwap(sdcInitial, variables = c("THOUSEXP", "TFOODEXP"), missing = NA) 

## setting parameter R0 = 0.95 as no inputs have been specified.

## The input dataset consists of 2000 rows and 40 variables.
##   --> Categorical key variables: URBRUR, REGION, HHSIZE, OWNAGLAND, RELIG
##   --> Numerical key variables: LANDSIZEHA, TANHHEXP, TFOODEXP, TALCHEXP, TCLTHEXP, THOUSEXP, TFURNEXP, THLTHEXP, TTRANSEXP, TCOMMEXP, TRECEXP, TEDUEXP, TRESTHOTEXP, TMISCEXP, INCTOTGROSSHH, INCRMT, INCWAGE, INCFARMBSN, INCNFARMBSN, INCRENT, INCFIN, INCPENSN, INCOTHER
##   --> Weight variable: WGTPOP
##   --> Strata variable(s): strata_region
## ----------------------------------------------------------------------

## Information on categorical key variables:
## 
## Reported is the number, mean size and size of the smallest category >0 for recoded variables.
## In parenthesis, the same statistics are shown for the unmodified data.
## Note: NA (missings) are counted as seperate categories!

##  Key Variable Number of categories      Mean size            Size of smallest (>0)      
##        URBRUR                    2  (2)  1000.000 (1000.000)                   684 (684)
##        REGION                    6  (6)   333.333  (333.333)                   260 (260)
##        HHSIZE                   23 (23)    86.957   (86.957)                     1   (1)
##     OWNAGLAND                    4  (4)   531.667  (531.667)                   332 (332)
##         RELIG                    7  (7)   166.667  (166.667)                     7   (7)

## ----------------------------------------------------------------------

## Infos on 2/3-Anonymity:
## 
## Number of observations violating
##   - 2-anonymity: 115 (5.750%)
##   - 3-anonymity: 239 (11.950%)
##   - 5-anonymity: 497 (24.850%)
## 
## ----------------------------------------------------------------------

## Numerical key variables: LANDSIZEHA, TANHHEXP, TFOODEXP, TALCHEXP, TCLTHEXP, THOUSEXP, TFURNEXP, THLTHEXP, TTRANSEXP, TCOMMEXP, TRECEXP, TEDUEXP, TRESTHOTEXP, TMISCEXP, INCTOTGROSSHH, INCRMT, INCWAGE, INCFARMBSN, INCNFARMBSN, INCRENT, INCFIN, INCPENSN, INCOTHER
## 
## Disclosure risk is currently between [0.00%; 0.00%]
## 
## Current Information Loss:
##   - IL1: 5538581.77
##   - Difference of Eigenvalues: -5636215810422230.000%
## ----------------------------------------------------------------------

Se ha comprobado que Rank swapping da buenos resultados con respecto al equilibrio entre la pérdida de información y la protección de los datos (Josep Domingo-Ferrer and Torra 2001). Rank swapping no es útil para variables con pocos valores diferentes o muchos valores perdidos, ya que el intercambio en ese caso no dará lugar a valores alterados. Además, si el intruso sabe a quién pertenece el valor más alto o más bajo de una variable específica (por ejemplo, los ingresos), el nivel de esta variable se revelará después de Rank swapping, porque los valores en sí no se alteran y los valores originales se revelan todos. Esto puede resolverse codificando por arriba y por abajo los valores más bajos y/o más altos.

Lectura recomendada de adición de Rank Swapping:
- Dalenius T. and Reiss S.P. 1978. Data-swapping: a technique for disclosure control (extended abstract). In Proc. ASA Section on Survey Research Methods. American Statistical Association, Washington DC, 191–194.
- Domingo-Ferrer J. and Torra V. 2001. “A Quantitative Comparison of Disclosure Control Methods for Microdata.” In Confidentiality, Disclosure and Data Access: Theory and Practical Applications for Statistical Agencies, edited by P. Doyle, J.I. Lane, J.J.M. Theeuwes, and L. Zayatz, 111–134. Amsterdam, North-Holland.
- Hundepool A., Van de Wetering A., Ramaswamy R., Franconi F., Polettini S., Capobianchi A., De Wolf P.-P., Domingo-Ferrer J., Torra V., Brand R. and Giessing S. 2007. μ-Argus User’s Manual version 4.1.

8.3.5 Shuffling (Barajado)

El shuffling introducido por (Muralidhar and Sarathy 2006) es similar al swapping, pero utiliza un modelo de regresión subyacente con las variables para determinar cuáles se intercambian. El shuffling puede utilizarse para variables continuas y es un método determinista. El shuffling mantiene las distribuciones marginales en los datos barajados. Sin embargo, shuffling requiere una clasificación completa de los datos, que puede ser muy intensiva desde el punto de vista computacional para grandes conjuntos de datos con múltiples variables.

El método se explica en detalle en (Muralidhar and Sarathy 2006). La idea es clasificar a los individuos en función de sus variables originales. A continuación, se ajusta un modelo de regresión con las variables a proteger como regresores y un conjunto de variables que predicen bien esta variable (es decir, con las que están correlacionadas) como regresores. Este modelo de regresión se utiliza para generar \(n\) valores sintéticos (predichos) para cada variable que hay que proteger. Estos valores generados también se ranquean y cada valor original se sustituye por otro valor original con el rango que corresponde al ranking del valor generado. Esto significa que todos los valores originales estarán en los datos. La Tabla 8.14 presenta un ejemplo simplificado del método shuffling. En este ejemplo no se especifican los regresores.

Tabla 8.14: Métodos de agrupación para la microagregación que son implementados en sdcMicro

ID	Ingreso (orig.)	Rango (orig.)	Ingreso (pred.)	Rango (pred.)	Valores barajados
1	2,300	2	2,466.56	4	2,345
2	2,434	6	2,583.58	7	2,543
3	2,123	1	2,594.17	8	2,643
4	2,312	3	2,530.97	6	2,434
5	6,045	10	5,964.04	10	6,045
6	2,345	4	2,513.45	5	2,365
7	2,543	7	2,116.16	1	2,123
8	2,854	9	2,624.32	9	2,854
9	2,365	5	2,203.45	2	2,300
10	2,643	8	2,358.29	3	2,312

Se recomienda el uso del método “ds” (el método por defecto de shuffling en sdcMicro) (Matthias Templ Bernhard Meindl and Kowarik 2014). En el argumento “form” debe especificarse una función con regresores para las variables a proteger. Al menos dos regresores deben especificarse y estos deben tener poder predictivo para las variables a predecir. Esto puede comprobarse con medidas de bondad de ajuste como el \(R^2\) de la regresión. El \(R^2\) solo capta las relaciones lineales, pero estas son también las únicas relaciones que capta el modelo de regresión lineal utilizado para el shuffling. A continuación, se presenta un ejemplo para barajar las variables de gasto, que se predicen mediante el gasto total de los hogares y el tamaño de estos.

8.3.5.1

Bloque 8.24 Shuffling usando una ecuación de regresión especificada

# Evaluar el R-cuadrado (bondad de ajuste) del modelo de regresión
summary(lm(file, form = TFOODEXP + TALCHEXP + TCLTHEXP + THOUSEXP + TFURNEXP + THLTHEXP + TTRANSEXP + TCOMMEXP + TRECEXP + TEDUEXP + TRESTHOTEXP + TMISCEXP ~ TANHHEXP + HHSIZE)) 

## 
## Call:
## lm(formula = TFOODEXP + TALCHEXP + TCLTHEXP + THOUSEXP + TFURNEXP + 
##     THLTHEXP + TTRANSEXP + TCOMMEXP + TRECEXP + TEDUEXP + TRESTHOTEXP + 
##     TMISCEXP ~ TANHHEXP + HHSIZE, data = file)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -3.92e-10 -5.00e-12 -4.00e-12 -3.00e-12  3.90e-08 
## 
## Coefficients:
##              Estimate Std. Error   t value Pr(>|t|)    
## (Intercept) 2.853e-10  8.003e-12 3.565e+01   <2e-16 ***
## TANHHEXP    1.000e+00  1.075e-16 9.300e+15   <2e-16 ***
## HHSIZE      3.366e-13  1.087e-12 3.100e-01    0.757    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.794e-10 on 10571 degrees of freedom
## Multiple R-squared:      1,  Adjusted R-squared:      1 
## F-statistic: 4.975e+31 on 2 and 10571 DF,  p-value: < 2.2e-16

# Shuffling utilizando la ecuación de regresión especificada
sdcInitial <- shuffle(sdcInitial, method="ds", 
                      form = TFOODEXP + TALCHEXP + TCLTHEXP + THOUSEXP + 
                        TFURNEXP + THLTHEXP + TTRANSEXP + TCOMMEXP + 
                        TRECEXP + TEDUEXP + TRESTHOTEXP + TMISCEXP ~ TANHHEXP + HHSIZE) 

Lectura recomendada de shuffling:
- K. Muralidhar and R. Sarathy. 2006.”Data shuffling - A new masking approach for numerical data,” Management Science, 52, 658-670.

8.3.6 Comparación de PRAM, Rank swapping y Shuffling

PRAM, Rank swapping y Shuffling son métodos perturbativos, es decir, cambian los valores de los registros individuales y se utilizan principalmente para las variables continuas. Tras el rank swapping y shuffling, todos los valores originales están contenidos en el conjunto de datos tratado, pero pueden asignarse a otros registros. Esto implica que las tabulaciones univariantes no se modifican. Esto también se mantiene en la expectativa de PRAM, si se elige una matriz de transición que tenga la propiedad invariante.

La elección de un método se basa en la estructura a preservar en los datos. En los casos en los que el modelo de regresión se ajusta a los datos, el shuffling funcionaría muy bien, ya que debería haber suficientes regresores (continuos) disponibles. El rank swapping funciona bien si hay suficientes categorías en las variables. Se prefiere PRAM si el método de perturbación debe aplicarse solo a una o pocas variables; la ventaja es la posibilidad de especificar restricciones en la matriz de transición y aplicar PRAM solo dentro de los estratos, que pueden ser definidos por el usuario.

8.4 Anonimización del identificador indirecto de tamaño del hogar

El tamaño de un hogar es un identificador importante, especialmente para los hogares grandes³⁵. Sin embargo, la supresión de la variable de tamaño real, si está disponible (por ejemplo, el número de miembros del hogar), no basta para eliminar esta información del conjunto de datos, ya que un simple recuento de los miembros del hogar para un hogar concreto permitirá reconstruir esta variable siempre que haya un identificador del hogar en los datos. En cualquier caso, los hogares de un tamaño muy grande o con una clave única o especial (es decir, una combinación de valores de identificadores indirectos) deben comprobarse manualmente. Una forma de tratarlos es eliminar estos hogares del conjunto de datos antes de su publicación. Otra posibilidad es dividir los hogares, pero hay que tener cuidado de suprimir o cambiar los valores de estos hogares para evitar que un intruso entienda inmediatamente que estos hogares han sido divididos y los reconstruya combinando los dos hogares con los mismos valores.

8.5 Resumen de métodos SDC

Tabla 8.15: Métodos de agrupación para la microagregación que son implementados en sdcMicro

Métodos	Técnicas	Ventajas	Desventajas	Tipo de datos
Perturbativos	PRAM	Aplicar a subgrupos del conjunto de datos. Probabilidad positiva de un match con un individuo erróneo. Seleccionar la matriz de transición y probabilidad. Útil con muchas variables y/o alta pérdida de información.	Modificación de datos originales, se intercambian características. Mayor complejidad y posibilidad de error (seleccionar estratos). Aparenta que no hay anonimización. En el caso de las encuestas por muestreo, cada observación puede tener un peso muestral diferente, por lo que, después de la generalización, no se garantiza la coherencia.	Categórico
Perturbativos	Microagregación	Sencilla de comprender y aplicar. Versión univariada implica baja pérdida de información. Versión multivariada permite disminuir bastante el riesgo. Todos los valores originales están contenidos en la data tratada (distribuciones univariadas no cambian). Evita la introducción de inconsistencias que requieran edición.	Trade-off entre pérdida de información y disminución de riesgo según si se aplica de forma univariado o multivariada.	Continuo
Perturbativos	Adición de ruido	Puede añadir ruido de forma univariada o bivariada. Sencilla de comprender y aplicar.	Puede mantener niveles altos riesgos, no permite medir los riesgos post-aplicación. Variable de número enteros puede pasar a tener decimales (por ejemplo, 3,5 hijos). Puede incrementar rango de valores de variable. Necesaria edición posterior a la anonimización.	Continuo
Perturbativos	Shuffling (Barajado)	Todos los valores originales están contenidos en la data tratada (distribuciones univariadas no cambian). Permite mantener relaciones multivariadas.	Requiere una clasificación completa de los datos, que puede ser computacionalmente muy intensiva para grandes conjuntos de datos con varias variables. Necesita regresión lineal (deben cumplirse supuestos y la recta ajustar bien) La técnica requiere al menos dos variables cuantitativas en la fórmula de la función.	Continuo
Perturbativos	Rank swapping (Intercambio de rangos)	Todos los valores originales están contenidos en la data tratada (distribuciones univariadas no cambian). Sencilla de comprender y aplicar. Permite mantener relaciones multivariadas. Baja pérdida de información.	Reduce rango de valores mínimos y máximos. Puede mantener niveles altos de riesgos.	Continuo
No perturbativos	Supresión local	Quitar datos atípicos. Seleccionar datos a eliminar según importancia.	No es útil para variables continuas ni con alto número de categorías. Con alto número de variables o categorías puede no lograr solución. Limitación de algoritmo en librería sdcMicro. Observaciones con variables suprimidas quedan con valor perdido.	Categórico
No perturbativos	Recodificación Global	Se disminuye información, pero manteniendo estructura y relaciones.	Pérdida de información continua al categorizar para estimación de modelos. Cambia nivel de medición de variables continuas a ordinales o categóricas.	Continuo y categórico
No perturbativos	Codificación superior e inferior	Se pierde menos información que con recodificación global, permite agrupar solo las colas de la distribución.	Menor nivel de anonimización, se requiere evaluar trade-off entre ambos métodos.	Continuo y categórico

Referencias

Benschop, Thijs, Cathrine Machingauta, and Matthew Welch. 2019. “Statistical Disclosure Control: A Practice Guide.” https://sdcpractice.readthedocs.io/en/latest/.

Brand, Ruth. 2002. “Microdata Protection Through Noise Addition.” In Inference Control in Statistical Databases: From Theory to Practice, edited by Josep Domingo-Ferrer, 97–116. Berlin, Heidelberg: Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-47804-3_8.

Domingo-Ferrer, Josep, Josep Mateo-Sanz, Anna Oganian, and Aánge Torres. 2002. “On the Security of Microaggregation with Individual Ranking: Analytical Attacks.” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 10 (October): 477–92. https://doi.org/10.1142/S0218488502001594.

Domingo-Ferrer, Josep, and Vicenc Torra. 2005. “Ordinal, Continuous and Heterogeneous k -Anonymity Through Microaggregation.” Data Mining and Knowledge Discovery 11 (September): 195–212. https://doi.org/10.1007/s10618-005-0007-5.

Domingo-Ferrer, Josep, and Vicenç Torra. 2001. “A Quantitative Comparison of Disclosure Control Methods for Microdata.” Confidentiality, Disclosure and Data Access: Theory and Practical Applications for Statistical Agencies, January.

Hundepool, A., J. Domingo-Ferrer, L. Franconi, S. Giessing, E. S. Nordholt, K. Spicer, and P. P. de Wolf. 2012. Statistical Disclosure Control. Wiley Series in Survey Methodology. Wiley. https://books.google.cl/books?id=9W4EywAACAAJ.

Kim, J, and W Winkler. 2003. “Multiplicative Noise for Masking Continuous Data.” Statistics 1 (9): 1–18. https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=7f62f83435f2c1b78855c282b1cd10c9f6e65a9e.

Matthias Templ, Alexander Kowarik, Bernhard Meindl, and Shuang Chen. 2014. “Introduction to Statistical Disclosure Control ( SDC ).” In. http://www.ihsn.org/home/software/disclosure-control-toolbox.

Matthias Templ, Bernhard Meindl, and Alexander Kowarik. 2014. “Introduction to Statistical Disclosure Control ( SDC ).” In. http://www.ihsn.org/home/software/disclosure-control-toolbox.

Muralidhar, Krishnamurty, and Rathindra Sarathy. 2006. “Data Shuffling: A New Masking Approach for Numerical Data.” Management Science 52 (5): 658–70. http://www.jstor.org/stable/20110544.

Wolf, Peter-Paul de. 2015. “Public Use Files of EU-SILC and EU-LFS Data.” Joint UNECE/Eurostat Work Session on Statistical Data Confidentiality, Helsinki, Finland, 1–10. http://www.ksh.hu/statszemle_archive/2015/2015_11-12/2015_11-12_1140_2.pdf.

---

21. Este enfoque sólo funciona para variables semicontinuas, porque en el caso de las variables continuas, puede haber valores que se encuentren entre el límite inferior del intervalo y el límite inferior del intervalo menos el número menor. Por ejemplo, utilizando este método para los ingresos, tendríamos un intervalo (9999, 19999↩︎

22. Aquí, el objeto sdcMicro “sdcIntial” contiene un conjunto de datos con 2.500 individuos y 103 variables. Seleccionamos cinco identificadores indirectos: “sizeRes”, “edad”, “sexo”, “región” y “etnia”.↩︎

23. Esto puede evaluarse con medidas de utilidad.↩︎

24. I2D2 es un conjunto de datos relacionados con el mercado laboral.↩︎

25. En este ejemplo y en los siguientes de esta sección, el objeto sdcMicro “sdcIntial” contiene un conjunto de datos con 2.000 individuos y 39 variables. Seleccionamos cinco identificadores indirectos categóricos y 9 variables para PRAM: “ROOF”, “TOILET”, “WATER”, “ELECTCON”, “FUELCOOK”, “OWNMOTORCYCLE”, “CAR”, “TV” y “LIVESTOCK”. Estas variabels PRAM se seleccionaron en función de los requisitos de este conjunto de datos concreto y con fines ilustrativos.↩︎

26. El método PRAM en sdcMicro a veces produce el siguiente error: Error in factor(xpramed, labels = lev) : invalid ‘labels’; length 6 should be 1 or 5. En algunas circunstancias, cambiar la semilla puede resolver este error.↩︎

27. Esto también puede lograrse con matrices de transición multidimensionales. En ese caso, la probabilidad no se especifica para “masculino” -> “feminino”, sino para “masculino” + ” rural ” -> “feminino” + ” rural ” y para “masculino” + “urbano” -> “feminino” + “urbano”. Esto no está implementado en sdcMicro, pero se puede lograr mediante PRAMming masculino y feminino por separado. En este ejemplo, esto podría hacerse especificando el género como variable de estrato en la función pram() de sdcMicro.↩︎

28. La microagregación también se puede utilizar para datos categóricos, siempre que exista la posibilidad de formar grupos y se pueda calcular una sustitución agregada para los valores del grupo. Este es el caso de las variables ordinales.↩︎

29. En este caso, todos los grupos pueden tener diferentes tamaños (es decir, número de individuos en un grupo). En la práctica, la búsqueda de grupos homogéneos se simplifica imponiendo tamaños de grupo iguales para todos los grupos.↩︎

30. En este ejemplo y en los siguientes de esta sección, el objeto sdcMicro “sdcIntial” contiene un conjunto de datos con 2.000 individuos y 39 variables. Seleccionamos cinco identificadores indirectos categóricos y tres identificadores indirectos continuos: “INC”, “EXP” y “WEALTH”.↩︎

31. Además, la homogeneidad en los grupos será generalmente menor, lo que dará lugar a cambios mayores, a una mayor protección, también una mayor pérdida de información, a menos que la variable de estrato esté correlacionada con la variable de microagregación.↩︎

32. Los valores habituales de \(\alpha\) están entre 0,5 y 2. El valor predeterminado en la función addNoise() de sdcMicro es 150, que es demasiado grande para la mayoría de los conjuntos de datos; el nivel de ruido debe establecerse en el argumento “noise”.↩︎

33. En este ejemplo y en los siguientes de esta sección, el objeto sdcMicro “sdcIntial” contiene un conjunto de datos con 2.000 individuos y 39 variables. Seleccionamos cinco identificadores indirectos categóricos y 12 identificadores indirectos continuos. Se trata de los componentes de gasto “TFOODEXP”, “TALCHEXP”, “TCLTHEXP”, “THOUSEXP”, “TFURNEXP”, “THLTHEXP”, “TTRANSEXP”, “TCOMMEXP”, “TRECEXP”, “TEDUEXP”, “TRESTHOTEXP”, “TMISCEXP”.↩︎

34. La prueba de Shapiro-Wilk se implementa en la función shapiro.test() del paquete stats en R. La prueba de Jarque-Bera tiene varias implementaciones en R, por ejemplo, en la función jarque.bera.test() del paquete tseries.↩︎

35. En este caso, todos los grupos pueden tener diferentes tamaños (es decir, número de individuos en un grupo). En la práctica, la búsqueda de grupos homogéneos se simplifica teniendo tamaños de grupo iguales para todos los grupos.↩︎